Question

Cho đường tròn (O) có điểm A nằm ngoài đường tròn lấy lần lượt AB, AC là hai tiếp tuyến

b/ Vẽ đường kính CD của (O), gọi E là giao điểm của AD và (O), biết E khác D. CM: AB^2= AD.AE

c/Gọi H là giao điểm của AO và BC, vẽ đường kính BF của (O). Cm 3 điểm E, H, F thẳng hàng

 

Giúp mình vs ạ :3

Answer 1

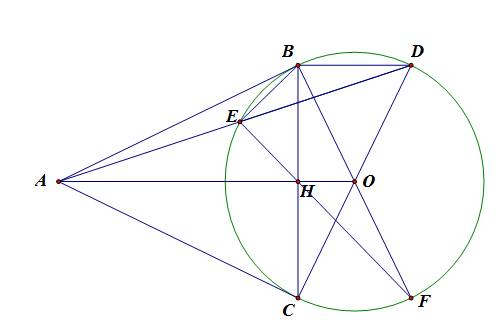
b, Xét ΔABE và ΔADB, có: \(\angle ABE=\angle ADB,\angle A\) chung 

⇒ ΔABE ∼ ΔADB (g.g) ⇒ \(\dfrac{AB}{AE}=\dfrac{AD}{AB}\Rightarrow AB^2=AD.AE\)

c, Vì BF là đường kính của (O) nên \(\angle FEB=90^o \Rightarrow FE \ \bot \ EB\) tại E.

ΔABO vuông tại H, có BH là đường cao ⇒ \(AB^2=AH.AO\)

\(\Rightarrow AD.AE=AH.AO \Rightarrow \dfrac{AE}{AH}= \dfrac{AO}{AD} \Rightarrow \Delta AHE \sim \Delta ADO\) (c.g.c)

\(\Rightarrow \angle AEH=\angle AOD \Leftrightarrow \angle HED=\angle AOC=\angle HOC\)

Ta có: \(\angle HEB=\angle HED+\angle DEB=\angle HOC+\angle DCB=90^o\)

\(\Rightarrow HE\ \bot \ EB\); mà \(FE\ \bot \ EB\)

\(\Rightarrow \) E, H, F thẳng hàng.