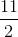Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có A(3;4), đường trung trực cạnh BC có phương trình 3x−y+1=0, đường trung tuyến kẻ từ C có phương trình 2x−y+5=0. Các mệnh đề sau đúng hay sai?
Mệnh đề a) Gọi M là trung điểm cạnh BC . Khi đó M(9;39)
b) Phương trình đường thẳng BC là: x+3y−63=0
c) Tọa độ đỉnh C là C(-1;3)
d) Tọa độ đỉnh B là B (15/7 ;142/7 )
Do M thuộc trung trực BC nên tọa độ dạng \(M\left(m;3m+1\right)\)
Gọi d: \(2x-y+5=0\) là trung tuyến kẻ từ C
Theo tính chất trọng tâm tam giác, ta có: \(d\left(A;d\right)=2d\left(M;d\right)\)
\(\Rightarrow\dfrac{\left|2.3-4+5\right|}{\sqrt{2^2+\left(-1\right)^2}}=2.\dfrac{\left|2m-\left(3m+1\right)+5\right|}{\sqrt{2^2+\left(-1\right)^2}}\)
\(\Rightarrow\left|4-m\right|=\dfrac{7}{2}\Rightarrow\left[{}\begin{matrix}m=\dfrac{1}{2}\\m=\dfrac{15}{2}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}M\left(\dfrac{1}{2};\dfrac{5}{2}\right)\\M\left(\dfrac{15}{2};\dfrac{47}{2}\right)\end{matrix}\right.\)
Do M và A nằm khác phía so với d \(\Rightarrow M\left(\dfrac{15}{2};\dfrac{47}{2}\right)\)
Đường thẳng BC qua M và vuông góc d nên nhận (1;3) là 1 vtpt
Phương trình BC:
\(1\left(x-\dfrac{15}{2}\right)+3\left(y-\dfrac{47}{2}\right)=0\Leftrightarrow x+3y-78=0\)
C là giao điểm BC và d nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}x+3y-78=0\\2x-y+5=0\end{matrix}\right.\) \(\Rightarrow C\left(9;23\right)\)
M là trung điểm BC \(\Rightarrow\left\{{}\begin{matrix}x_B=2x_M-x_C=6\\y_B=2y_M-y_C=24\end{matrix}\right.\)
\(\Rightarrow B\left(6;24\right)\)
a) Gọi M là trung điểm của BC. Điểm M có tọa độ là trung bình của tọa độ hai điểm B và C.
Tọa độ điểm B: Giao điểm của đường thẳng BC và đường thẳng trung tuyến từ C, giải hệ phương trình:
\[
\begin{cases}
3x - y + 1 = 0 \\
2x - y + 5 = 0
\end{cases}
\]
Tìm B(15/7; 88/7).
Do B(15/7; 88/7) và C(-1; 3) nên tọa độ trung điểm M của BC là \((\frac{15/7 - 1}{2}, \frac{88/7 + 3}{2}) = (\frac{1}{7}, \frac{101}{14})\).
Do đó, mệnh đề a) là **Sai**.
b) Để tìm phương trình của đường thẳng BC, ta cần biết một điểm trên đường thẳng và hệ số góc của nó.
Điểm B đã được tìm ở câu trên. Ta cần tính góc nghiêng của BC.
Góc nghiêng của đường thẳng BC chính là góc nghiêng của đường trung tuyến kẻ từ C, vì đường trung trực cắt đường trung tuyến vuông góc. Vậy, ta cần tính góc giữa đường trung tuyến và trục hoành.
Góc giữa đường thẳng có hệ số góc là \(m\) và trục hoành là \(tan^{-1}(m)\).
Hệ số góc của đường trung tuyến là \(m_1 = -\frac{2}{3}\), vậy \(tan^{-1}(-\frac{2}{3})\) là góc giữa đường thẳng BC và trục hoành.
Phương trình đường thẳng BC là:
\[
\frac{y - y_1}{x - x_1} = -\frac{2}{3}
\]
Thay vào \(x_1 = 15/7, y_1 = 88/7\), ta có:
\[
\frac{y - \frac{88}{7}}{x - \frac{15}{7}} = -\frac{2}{3}
\]
Từ đó, ta tính được phương trình của BC là \(x + 3y - 63 = 0\). Vậy, mệnh đề b) là **Đúng**.
c) Tọa độ đỉnh C đã được cho là C(-1;3). Vậy, mệnh đề c) là **Đúng**.
d) Để tìm tọa độ đỉnh B, ta đã tính ở câu trên là B(15/7; 88/7). Vậy, mệnh đề d) là **Sai**.
**Kết luận:**
- Mệnh đề a) Sai.
- Mệnh đề b) Đúng.
- Mệnh đề c) Đúng.
- Mệnh đề d) Sai.
Rồi kết luận là như thế nào vậy ạ chả heh gì????