a.
Thay gốc tọa độ \(O\left(0,0\right)\) vào pt \(\Delta\) ta được:
\(3.0-4.0+4=0\Leftrightarrow4=0\) (ko thỏa mãn)
Vậy O không thuộc \(\Delta\) hay \(\Delta\) ko đi qua gốc tọa độ
b.
Đường tròn (C) có tâm \(I\left(1;-2\right)\) và bán kính \(R=3\)
Khoảng cách từ I đến \(\Delta\) là:
\(d\left(I;\Delta\right)=\dfrac{\left|3.1-4.\left(-2\right)+4\right|}{\sqrt{3^2+\left(-4\right)^2}}=\dfrac{15}{5}=3=R\)
\(\Rightarrow\Delta\) tiếp xúc với (C)
c.
Do M là giao điểm \(\Delta\) với Oy \(\Rightarrow x_M=0\)
\(\Rightarrow3.0-4y_M+4=0\Rightarrow y_M=1\)
\(\Rightarrow M\left(0;1\right)\)
\(\Rightarrow\overrightarrow{MI}=\left(1;-3\right)\Rightarrow MI=\sqrt{1^2+\left(-3\right)^2}=\sqrt{10}\)




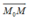 cùng phương với
cùng phương với