Đáp án A
Phương pháp:
Cho ![]() ;
; ![]() nhận
n
1
→
=
a
1
;
b
1
;
c
1
;
n
2
→
=
a
2
;
b
2
;
c
2
lần lượt là các VTPT. Khi đó, góc giữa hai mặt phẳng
nhận
n
1
→
=
a
1
;
b
1
;
c
1
;
n
2
→
=
a
2
;
b
2
;
c
2
lần lượt là các VTPT. Khi đó, góc giữa hai mặt phẳng
α ; β được tính: cos α ; β = cos n 1 → ; n 2 → = n 1 → . n 2 → n 1 → n 2 →
Với 0 0 ≤ α ≤ 90 0 ⇒ α m i n ⇔ cos α m a x
Cách giải:
(P): x + 2y – 2z +2018 = 0 có 1 VTPT: n 1 → = 1 ; 2 ; - 2
(Q): x + my + (m – 1)z + 2017 = 0 có 1 VTPT: n 2 → = 1 ; m ; m - 1
Góc giữa hai mặt phẳng (P) và (Q):
cos P ; Q = cos n 1 → ; n 2 → = n 1 → . n 2 → n 1 → n 2 →
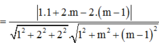
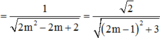
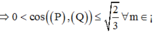
Với 0 0 ≤ α ≤ 90 0 ⇒ α m i n ⇔ cos α m a x
=>((P),(Q))min khi và chỉ khi 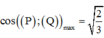
![]()
Khi đó, 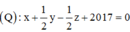
![]()
Ta thấy: ![]()
![]()

