Bài 3: Cấp số cộng
a) Dãy số bị chặn dưới vì un = 2n2 -1 ≥ 1 với mọi n ε N* và không bị chặn trên vì với số M dương lớn bất kì, ta có 2n2 -1 > M <=> n > 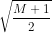 .
tức là luôn tồn tại n ≥
.
tức là luôn tồn tại n ≥ 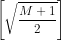 + 1 để 2
+ 1 để 2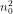 - 1 > M.
b) Dễ thấy un > 0 với mọi n ε N*
Mặt khác, vì n ≥ 1 nên n2 ≥ 1 và 2n ≥ 2.
Do đó n(n + 2) = n2 + 2n ≥ 3, suy ra
- 1 > M.
b) Dễ thấy un > 0 với mọi n ε N*
Mặt khác, vì n ≥ 1 nên n2 ≥ 1 và 2n ≥ 2.
Do đó n(n + 2) = n2 + 2n ≥ 3, suy ra 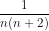
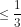 .
Vậy dãy số bị chặn 0 < un
.
Vậy dãy số bị chặn 0 < un 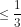 với mọi n ε N*
c) Vì n ≥ 1 nên 2n2 - 1 > 0, suy ra
với mọi n ε N*
c) Vì n ≥ 1 nên 2n2 - 1 > 0, suy ra 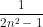 > 0
Mặt khác n2 ≥ 1 nên 2n2 ≥ 2 hay 2n2 - 1≥ 1, suy ra
> 0
Mặt khác n2 ≥ 1 nên 2n2 ≥ 2 hay 2n2 - 1≥ 1, suy ra 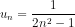 ≤ 1.
Vậy 0 < un ≤ 1, với mọi n ε N* , tức dãy số bị chặn.
d) Ta có: sinn + cosn = √2sin(n +
≤ 1.
Vậy 0 < un ≤ 1, với mọi n ε N* , tức dãy số bị chặn.
d) Ta có: sinn + cosn = √2sin(n + 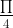 ), với mọi n. Do đó:
-√2 ≤ sinn + cosn ≤ √2 với mọi n ε N*
Vậy -√2 < un < √2, với mọi n ε N* .
), với mọi n. Do đó:
-√2 ≤ sinn + cosn ≤ √2 với mọi n ε N*
Vậy -√2 < un < √2, với mọi n ε N* .
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Trong các dãy số \(\left(u_n\right)\) sau đây, dãy số nào là cấp số cộng ?
a) \(u_n=3n-1\)
b) \(u_n=2^n+1\)
c) \(u_n=\left(n+1\right)^2-n^2\)
d) \(\left\{{}\begin{matrix}u_1=3\\u_{n+1}=1-u_n\end{matrix}\right.\)
Cho dãy số \(\left(u_n\right)\) là một cấp số cộng có \(u_1\) = 4, công sai d = -3 và \(u_n\) = -41. Tìm n?
Cho dãy số \(\left(u_n\right)\) với \(u_n=1-7n\)
a) Khảo sát tính tăng, giảm của dãy số
b) Chứng minh dãy số trên là cấp số cộng. Lập công thức truy hồi của dãy số
c) Tính tổng 100 số hạng đầu của dãy số
Chứng minh , kiểm tra 1 dãy số có là cấp số cộng hay không ? xác định U1 , d
a , \(\left\{{}\begin{matrix}u_1\\u_n+1=u_n-n\end{matrix}\right.\)
b , \(\left\{{}\begin{matrix}u_1=a\\u_n+1=5\end{matrix}\right.\) tìm a để d số là cấp số cộng
trong các dãy số (Un) sau. dãy nào là cấp số cộng
a, \(u_n=v_n-v_{n-1}\) với \(v_n=\left(2n+1\right)^2\)
b, \(u_n=\left(-1\right)^n+2n\)
c, \(\left\{{}\begin{matrix}u_n\\u_{n+1}=1-u_n\end{matrix}\right.=3\) với \(n\ge1\)
Tìm số hạng đầu \(u_1\) và công sai \(d\in Z\) của cấp số cộng \(\left(u_n\right)\) biết
a) \(\left\{{}\begin{matrix}u_6=8\\u_2^2+u_4^2=16\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}u_5=18\\4S_n=S_{2n}\end{matrix}\right.\)
Bài: tìm số hạng đầu, công sai của cấp số cộng \(\left(u_n\right)\):
a) \(\left\{{}\begin{matrix}u_2-u_3+u_5=10\\u_4+u_6=26\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}u_2-u_6+u_4=-7\\u_8-2u_7=2u_4\end{matrix}\right.\)
c) \(\left\{{}\begin{matrix}u_7-u_3=8\\u_2.u_7=75\end{matrix}\right.\)
Cho dãy số (un) : \(0;\frac{1}{2};\frac{2}{3};\frac{3}{4};\frac{4}{5};....\) Số hạng tổng quát của dãy số (un) là :
A. \(u_n=\frac{n-1}{n}\)
B. \(u_n=\frac{n}{n+1}\)
C. \(u_n=\frac{n^2-n}{n+1}\)
D. \(u_n=\frac{n+1}{n+2}\)
Cho cấp số cộng \(\left(u_n\right)\) chứng minh nếu :
\(\dfrac{S_m}{S_n}=\dfrac{m^2}{n^2}\)
thì :
\(\dfrac{u_m}{u_n}=\dfrac{2m-1}{2n-1}\)

