Tương tự ta tìm được các hệ thức:
2BE = BA + BC – AC
2CF = CA + CB – AB
Tương tự ta tìm được các hệ thức:
2BE = BA + BC – AC
2CF = CA + CB – AB
Trên hình 82, tam giác ABC ngoại tiếp đường tròn (O).
a) Chứng minh rằng:
2AD = AB + AC – BC
b) Tìm các hệ thức tương tự như hệ thức ở câu a).
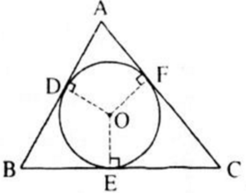
Hình 82
Trên hình 82, tam giác ABC ngoại tiếp đường tròn (O).
a) Chứng minh rằng:
2AD=AB+AC-BC.
b) Tìm các hệ thức tương tự hệ thức ở câu a).
Trên hình 82, tam giác ABC ngoại tiếp đường tròn (O).
Chứng minh rằng:
2AD = AB + AC – BC
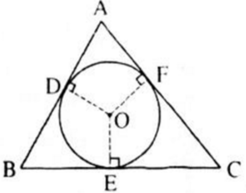
Hình 82
Độ dài các cạnh của một tam giác ABC vuông tại A, thỏa mãn các hệ thức sau:
BC = AB + 2a (1)
AC = 1/2.(BC + AB) (2)
a là một độ dài cho trước
Tam giác ABC nội tiếp được trong nửa hình tròn tâm O. Tính diện tích của phần thuộc nửa đường tròn nhưng ở ngoài tam giác đó
Câu 4(3,0đ). Cho tam giác ABC có góc A = 90 độ ngoại tiếp đường tròn (I;r). Gọi D, E, F lần lượt là các tiếp điểm trên BC, AB, AC.
a) Chứng minh tứ giác AEIF là hình vuông.
b) Gọi M, N thứ tự là tâm các đường tròn ngoại tiếp các tam giác ABD và ACD. Chứng
minh tứ giác AMDN nội tiếp.
c ) gọi S là diện tích của tam giác ABC . Chứng minh \(\sqrt{2S}\) -r ≤ \(\dfrac{BC}{2}\)
Mọi người giúp em phần c với ạ em cảm ơn mọi người nhiều
Cho tam giác ABC có đường cao AH, nội tiếp trong đường tròn tâm O, đường kính BC. Gọi E,D lần lượt là hình chiếu của H trên cạnh AB, AC.
a/ CMR: tứ giác ADHE là hình chữ nhật
b/ Chứng minh AB.AE=AD.AC
c/ Gọi I,J lần lượt k là tâm các đường tròn ngoại tiếp tam giác CDH,BEH.Xác định vị trí tương đối giữa các đường tròn (i) và (J) và (O)
d/ CMR: ID là tiếp tuyến của đường tròn ngoại tiếp tam giác AEH.
Cho tam giác ABC không cân ở A,gọi M là trung điểm cạnh BC, D là hình chiếu vuông góc của A trên BC, E và F lần lượt là các hình chiếu vuông góc của B và C trên đường kính AA' của đường tròn ngoại tiếp tam giác ABC
CMR: M là tâm đường tròn ngoại tiếp tam giác DEF
Cho tam giác ABC nhọn nội tiếp đường tròn O, có các đường cao AK,BI cắt nhau ở H.
a) Xác định tâm F của đường tròn ngoại tiếp tam giác BKI, tâm D của đường tròn ngoại tiếp tam giác IHF, tâm E của đường tròn ngoại tiếp tam giác AFC.
b)Cm: AEDF là hình bình hành.
Cho hình thang ABCD đáy lớn AD đáy nhỏ BC nội tiếp đường tròn tâm O. AB và CD kéo dài cắt nhau tại I. Các tiếp tuyến của đường tròn (O) tại B và D cắt nhau tại K.
a> C/m tứ giác BIKD nội tiếp
b> C/m IK//BC
c> Hình thang ABCD cần thêm điều kiện gì để tứ giác AIKD là hình bình hành. Khi đó c/m hệ thức: IC.IE=ID.CE( với E là giao điểm của BK và ID)
d> Vẽ hình bình hành BDKM, đường tròn ngoại tiếp tam giác BKM cắt đường tròn (O) tại điểm thứ 2N.C/m 3 điểm D,M,N thẳng hàng.