Xét tam giác OAC và tam giác OBD có:
góc OAC= góc OBD (gt)
OA=OB (gt)
góc O là góc chung
Do đó: tam giác OAC = tam giác OBD(g.c.g)
=> AC=BD
Vậy AC=BD
Xét ΔOAC và ΔOBD có:
Nên ΔOAC = ΔOBD (g.c.g)
Suy ra AC = BD
Xét tam giác OAC và tam giác OBD có:
góc OAC= góc OBD (gt)
OA=OB (gt)
góc O là góc chung
Do đó: tam giác OAC = tam giác OBD(g.c.g)
=> AC=BD
Vậy AC=BD
Xét ΔOAC và ΔOBD có:
Nên ΔOAC = ΔOBD (g.c.g)
Suy ra AC = BD
Cho góc xOy khác góc bẹt, Ot là tia phân giác của góc đó. Qua điểm H thuộc tia Ot, kẻ đường vuông góc với Ot, nó cắt Ox và Oy theo thứ tự ở A và B
a) Chứng minh rằng OA = OB
b) Lấy điểm C thuộc tia Ot, chứng minh rằng CA = CB và \(\widehat{OAC}=\widehat{OBC}\)
Trên hình 90, ta có OA=OB, ∠OAC=∠OBD. Chứng minh:
a) ∠ODB=∠OCA;
b)ID=IC;
c) OI là phân giác của góc DOC và OI⊥CD
Ta có : ΔABC có \(\widehat{C}=\widehat{B}\).Tia p/g BD,CE của \(\widehat{B}=\widehat{C}\) cắt nhau tại O
Từ O kẻ OH ⊥ AC,OK ⊥ AB
C/M : A) ΔBCD= ΔCBE
B)OB=OC
C)OH=OK
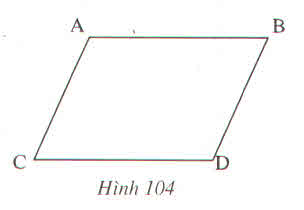
Trên hình 104 ta có AB // CD, AC // BD. Hãy chứng minh rằng AB = CD, AC = BD ?
Cho tam giác ABC có \(\widehat{B}=\widehat{C}\). Tia phân giác của góc A cắt BC tại D.
Chứng minh rằng :
DB = DC; AB = AC
Cho góc nhọn xoy trên ox lấy điểm A, B sao cho 0<OA<OB. Trên tia Oy lấy 2 điểm C, D
sao cho OA=OC, OB=OD. Gọi M là giao điểm của AD và BC, N là giao điểm của ON và BD. Chứng minh rằng:
a) △OAD bằng △OCB
b) △ADM bằng △CDM
c) OM là tia phân giác của góc xOy
d) ON ⊥ BD
Cho góc nhọn xoy trên tia õ lấy điểm A,C trên tia Oy lấy điểm B,D sao cho OA = OB , AC= BD A) cm AD = BC
Đề bài: Cho có
(góc
nhọn). Từ B hạ BH
vuông góc với AC, từ C hạ CK vuông góc với AB. Chứng minh rằng:
(1) và
cùng nhọn.
(2) BH = CK.
Cho tam giác ABC có \(\widehat{A}=60^0\). Các tia phân giác của các góc B, C cắt nhau ở I và cắt AC, AB theo thứ tự ở D, E. Chứng minh rằng ID = IE
Hướng dẫn : Kẻ tia phân giác của góc BIC