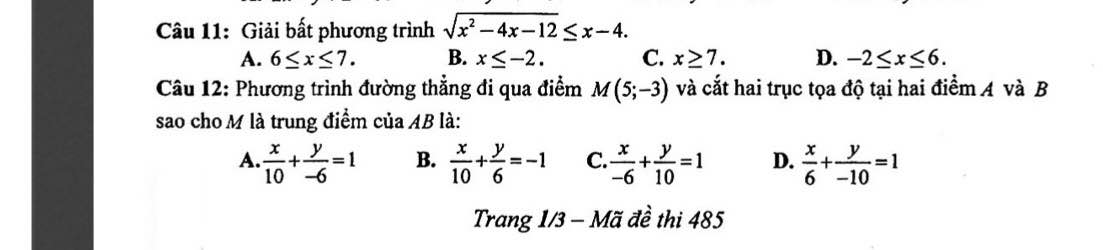a: \(0^0< \alpha< 90^0\)
=>\(tan\alpha>0\)
=>Đúng
b:
\(tan^2\alpha-tan\alpha-6=0\)
=>\(\left(tan\alpha-3\right)\left(tan\alpha+2\right)=0\)
=>Đúng
c: \(\left(tan\alpha-3\right)\left(tan\alpha+2\right)=0\)
=>\(\left[{}\begin{matrix}tan\alpha-3=0\\tan\alpha+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}tan\alpha=3\left(nhận\right)\\tan\alpha=-2\left(loại\right)\end{matrix}\right.\)
\(P=\dfrac{1}{cos^2a}+\dfrac{1}{sin^2\alpha}\)
\(=tan^2\alpha+1+cot^2\alpha+1\)
\(=tan^2\alpha+cot^2\alpha+2\)
=>Đúng
d: \(P=tan^2\alpha+cot^2\alpha+2=tan^2\alpha+\dfrac{1}{tan^2\alpha}+2\)
\(=3^2+\dfrac{1}{9}+2=11+\dfrac{1}{9}=\dfrac{100}{9}\)
=>Sai
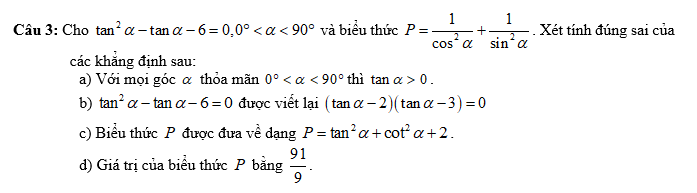





 Giải giúp mình phần trắc nghiệm với ạ
Giải giúp mình phần trắc nghiệm với ạ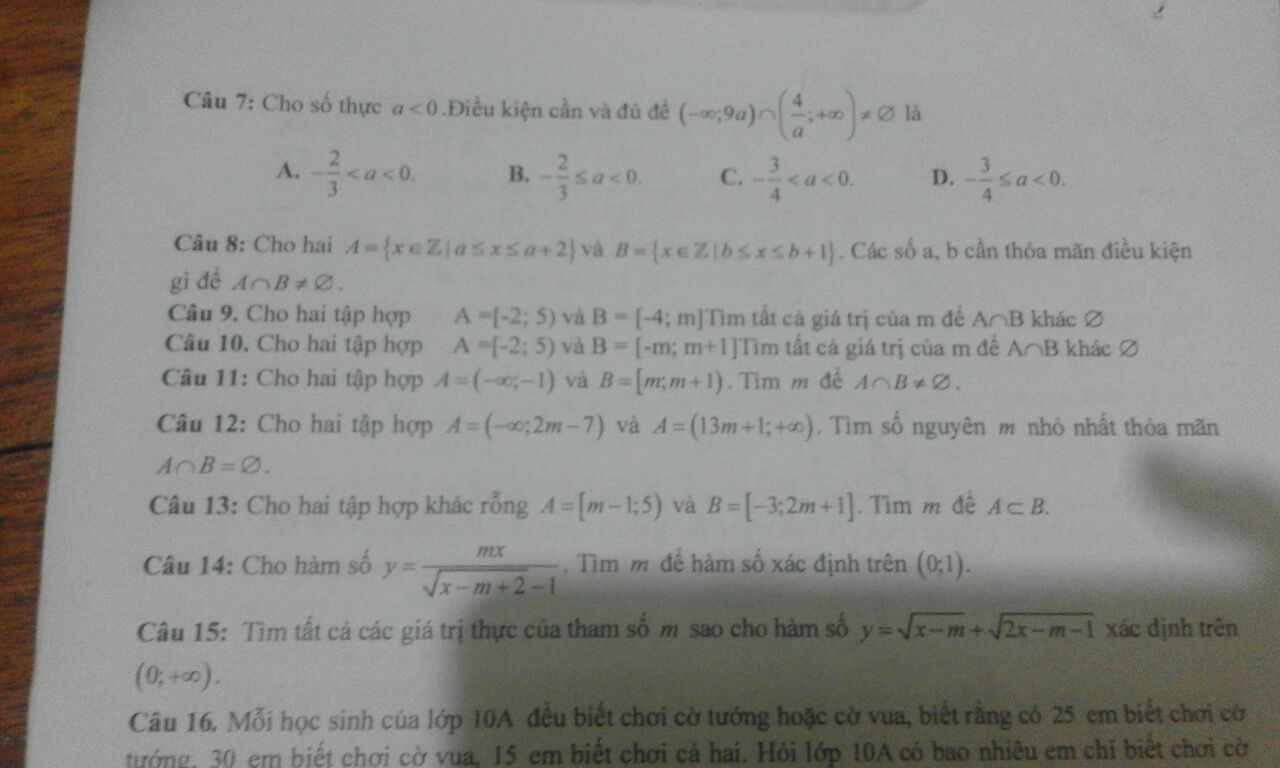 GIÚP MK VS!!! MAI MK PHẢI NỘP RỒI!!!!!!!!
GIÚP MK VS!!! MAI MK PHẢI NỘP RỒI!!!!!!!!