\(A=x^2+y^2-8x-y+68=\left(x-4\right)^2+\left(y-\dfrac{1}{2}\right)^2+\dfrac{207}{4}\ge\dfrac{207}{4}\)
\(minA=\dfrac{207}{4}\Leftrightarrow\)\(\left\{{}\begin{matrix}x=4\\y=\dfrac{1}{2}\end{matrix}\right.\)
\(A=x^2-8x+y^2-y+68\)
\(=x^2-8x+16+y^2-y+\dfrac{1}{4}+\dfrac{207}{4}\)
\(=\left(x-4\right)^2+\left(y-\dfrac{1}{2}\right)^2+\dfrac{207}{4}\ge\dfrac{207}{4}\forall x,y\)
Dấu '=' xảy ra khi x=4 và \(y=\dfrac{1}{2}\)



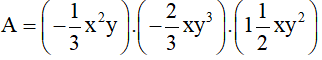
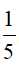 ; y = -1
; y = -1
