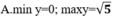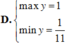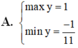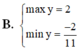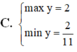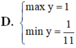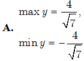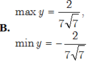\(-1< =sinx< =1\)
=>\(-2< =2\cdot sinx< =2\)
=>\(-2+3< =2\cdot sinx+3< =2+3\)
=>\(1< =2\cdot sinx+3< =5\)
=>\(\dfrac{2}{1}>=\dfrac{2}{2sinx+3}>=\dfrac{2}{5}\)
=>\(\dfrac{2}{5}< =y< =2\)
\(y_{min}=\dfrac{2}{5}\) khi sin x=1
=>\(x=\dfrac{\Omega}{2}+k2\Omega\)
\(y_{max}=2\) khi sin x=-1
=>\(x=-\dfrac{\Omega}{2}+k2\Omega\)