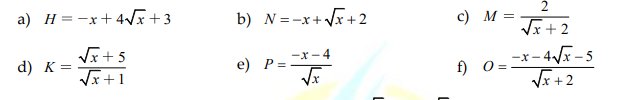a:
ĐKXĐ: x>=0
\(H=-x+4\sqrt{x}+3\)
\(=-\left(x-4\sqrt{x}-3\right)\)
\(=-\left(x-4\sqrt{x}+4-7\right)=-\left(\sqrt{x}-2\right)^2+7< =7\forall x>=0\)
Dấu '=' xảy ra khi \(\sqrt{x}-2=0\)
=>x=4
b: ĐKXĐ: x>=0
\(N=-x+\sqrt{x}+2\)
\(=-\left(x-\sqrt{x}-2\right)\)
\(=-\left(x-\sqrt[]{x}+\dfrac{1}{4}\right)+\dfrac{9}{4}\)
\(=-\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{9}{4}< =\dfrac{9}{4}\forall x\)
Dấu '=' xảy ra khi \(\sqrt{x}-\dfrac{1}{2}=0\)
=>\(x=\dfrac{1}{4}\)
c: ĐKXĐ: x>=0
\(\sqrt{x}+2>=2\forall x>=0\)
=>\(M=\dfrac{2}{\sqrt{x}+2}< =\dfrac{2}{2}=1\forall x\)>=0
Dấu '=' xảy ra khi x=0
d: ĐKXĐ: x>=0
\(K=\dfrac{\sqrt{x}+5}{\sqrt{x}+1}=\dfrac{\sqrt{x}+1+4}{\sqrt{x}+1}=1+\dfrac{4}{\sqrt{x}+1}\)
\(\sqrt{x}+1>=1\forall x>=0\)
=>\(\dfrac{4}{\sqrt{x}+1}< =\dfrac{4}{1}=4\forall x>=0\)
=>\(K=\dfrac{4}{\sqrt{x}+1}+1< =4+1=5\forall x>=0\)
Dấu '=' xảy ra khi x=0
e:
ĐKXĐ: x>0
\(P=\dfrac{-x-4}{\sqrt{x}}=-\sqrt{x}-\dfrac{4}{\sqrt{x}}=-\left(\sqrt{x}+\dfrac{4}{\sqrt{x}}\right)\)
\(\sqrt{x}+\dfrac{4}{\sqrt{x}}>=2\cdot\sqrt{\sqrt{x}\cdot\dfrac{4}{\sqrt{x}}}=4\)
=>\(P=-\left(\sqrt{x}+\dfrac{4}{\sqrt{x}}\right)< =-4\) với mọi x thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi \(\sqrt{x}=\dfrac{4}{\sqrt{x}}\)
=>\(\sqrt{x}^2=4\)
=>x=4(nhận)