Giải:
Để biểu thức xác định thì:
\(x^2-4\ge0\)
\(\Leftrightarrow x^2\ge4\)
\(\Leftrightarrow x\ge2\left(x=-2\right)\)
Vậy ...
biểu thức xác định khi
x2 - 4 ≥ 0
⇔ x2 ≥ 4
⇔ \(\left[{}\begin{matrix}x\ge2\\x\le-2\end{matrix}\right.\)
Giải:
Để biểu thức xác định thì:
\(x^2-4\ge0\)
\(\Leftrightarrow x^2\ge4\)
\(\Leftrightarrow x\ge2\left(x=-2\right)\)
Vậy ...
biểu thức xác định khi
x2 - 4 ≥ 0
⇔ x2 ≥ 4
⇔ \(\left[{}\begin{matrix}x\ge2\\x\le-2\end{matrix}\right.\)
1. tìm điều kiện để biểu thức sau xác định: a)√x2- 4x + 16
Tìm x để biểu thức sau được xác định :
a) \(\sqrt{\left|x\right|-1}\)
b) \(\sqrt{-\left|x+5\right|}\)
c_ \(\sqrt{\left|x-1\right|-3}\)
Tìm các giá trị của x để biểu thức sau có nghĩa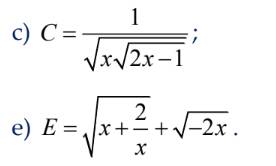
Bài 1: * Cho biểu thức A = 5x - \(\sqrt{4x^2-4x+1}\)
a, Rút gọn A
b, Tính giá trị của biểu thức A với x = -2
* Cho biểu thức B = 2x - \(\sqrt{x^2+4x+4}\)
a, Rút gọn B
b, Tính giá trị của biểu thức B để B = -10
* Cho biểu thức C = \(\frac{\sqrt{4x^2-4x+1}}{4x^2-1}\)
a, Rút gọn C
b, Tính giá trị của x để C = \(\frac{-1}{5}\)
c, Tính giá trị của x để C > 0
Tìm x để biểu thức sau xác định:
a) \(3+\sqrt{-\left(x+1\right)^2}\)
b) \(\dfrac{3x+9}{x^2-9}+\sqrt{x+1}\)
Tìm x để biểu thức sau xác định:
a) \(\sqrt{\left(x+2\right).\left(x-1\right)}\)
b) \(\sqrt{\dfrac{x-3}{2x-1}}\)
c) \(\sqrt{-x^2+2x-1^{ }}\)
Bài 1: * Cho biểu thức A = 5x - \(\sqrt{4x^2-4x+1}\)
a, Rút gọn A
b, Tính giá trị của biểu thức A với x = -2
* Cho biểu thức B = 2x - \(\sqrt{x^2+4x+4}\)
a, Rút gọn B
b, Tính giá trị của biểu thức B để B = -10
* Cho biểu thức C = \(\frac{\sqrt{4x^2-4x+1}}{4x^2-1}\)
a, Rút gọn C
b, Tính giá trị của x để C = \(\frac{-1}{5}\)
c, Tính giá trị của x để C > 0
tìm điều kiện của x để biểu thức xác định
1. \(\sqrt{x-2\sqrt{x-1}}\)
2. \(\sqrt{-\left|x+5\right|}\)
tìm min, max của các biểu thức sau
a, √ x2-2x+5
b, 2 + √x2-4x+5