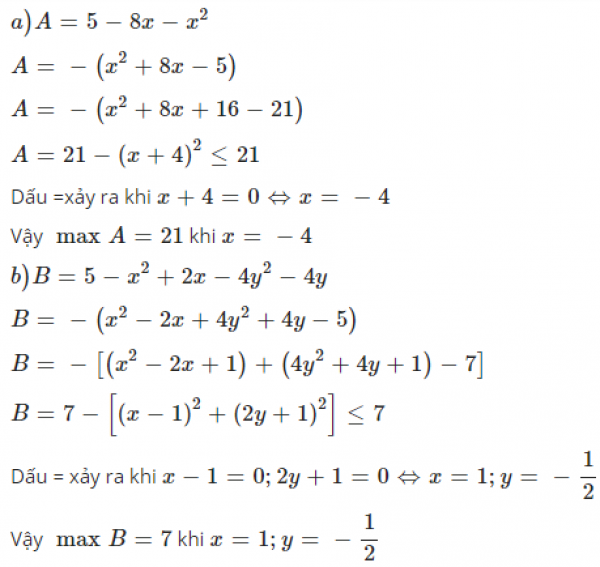a, \(A=-\left(x^2+8x+16-16\right)+5=-\left(x+4\right)^2+21\le21\forall x\)
Dấu ''='' xảy ra khi x = - 4
Vậy GTLN của A là 21 tại x = -4
b, \(B=-\left(x^2-2x+1\right)-\left(4y^2+4y+1\right)+7\)
\(=-\left(x-1\right)^2-\left(2y+1\right)^2+7\le7\forall x;y\)
Dấu ''='' xảy ra khi x = 1 ; y = -1/2
Vậy GTLN của B là 7 tại x = 1 ; y = -1/2
A = 5 − 8 x − x 2
= -(x2+8x+16)+21
= 21-(x+4)2
Với mọi x thì ( x + 4 ) 2 >= 0
=> 21−(x+4)2=<21 Hay A=<21
Để A=21 thì (x+4)2=0
=>x+4=0
=> x = − 4
Câu sau để anh nghĩ đã nhé
\(A=21-\left(16+8x+x^2\right)=21-\left(x+4\right)^2\)
Do \(\left(x+4\right)^2\ge0;\forall x\Rightarrow7-\left(x+4\right)^2\le7-0=7\)
\(A_{max}=21\) khi \(x=-4\)
\(B=7-\left(x^2-2x+1\right)-\left(4y^2+4y+1\right)=7-\left(x-1\right)^2-\left(2y+1\right)^2\)
Do \(\left\{{}\begin{matrix}\left(x-1\right)^2\ge0\\\left(2y+1\right)^2\ge0\end{matrix}\right.\) ; \(\forall x;y\Rightarrow7-\left(x-1\right)^2-\left(2y+1\right)^2\le7\)
\(B_{max}=7\) khi \(\left(x;y\right)=\left(1;-\dfrac{1}{2}\right)\)
\(a,A=5-8x-x^2\\ \Rightarrow A=-\left(x^2+8x-5\right)\\ \Rightarrow A=-\left(x^2+8x+16-21\right)\\ \Rightarrow A=-\left(x+4\right)^2+21\le21\)
Dấu "=" xảy ra \(\Leftrightarrow x=-4\)
Vậy \(A_{max}=21\Leftrightarrow x=-4\)
\(b,B=5-x^2+2x-4y^2-4y\\ \Rightarrow B=-x^2+2x-1-4y^2-4y-1+7\\ \Rightarrow B=-\left(x^2-2x+1\right)-\left(4y^2+4y+1\right)+7\\ \Rightarrow B=-\left(x-1\right)^2-\left(2y+1\right)^2+7\le7\)
Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-\dfrac{1}{2}\end{matrix}\right.\)
Vậy \(B_{max}=7\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-\dfrac{1}{2}\end{matrix}\right.\)