Chủ yếu em phân tích sao cho có nhân tử chung ra là được
a) \(\sqrt{5}-\sqrt{48}+5\sqrt{27}-\sqrt{45}=\sqrt{5}-\sqrt{16.3}+5\sqrt{9.3}-\sqrt{9.5}\)
\(=\sqrt{5}-4\sqrt{3}+15\sqrt{3}-3\sqrt{5}=11\sqrt{3}-2\sqrt{5}\)
b) \(2\sqrt{3}+\sqrt{48}-\sqrt{75}-\sqrt{243}=2\sqrt{3}+\sqrt{16.3}-\sqrt{25.3}-\sqrt{81.3}\)
\(=2\sqrt{3}+4\sqrt{3}-5\sqrt{3}-9\sqrt{3}=-8\sqrt{3}\)
c) \(3\sqrt{50}-2\sqrt{75}-4\dfrac{\sqrt{54}}{\sqrt{3}}-3\sqrt{\dfrac{1}{3}}\)
\(=3\sqrt{25.2}-2\sqrt{25.3}-4\sqrt{\dfrac{54}{3}}-\sqrt{9.\dfrac{1}{3}}=15\sqrt{2}-10\sqrt{3}-4\sqrt{18}-\sqrt{3}\)
\(=15\sqrt{2}-11\sqrt{3}-4\sqrt{9.2}=15\sqrt{2}-11\sqrt{3}-12\sqrt{2}=3\sqrt{2}-11\sqrt{3}\)
mấy câu dưới bạn làm tương tự thôi
d) Ta có: \(\dfrac{1}{5}\sqrt{50}-2\sqrt{96}-\dfrac{\sqrt{30}}{\sqrt{15}}+12\sqrt{\dfrac{1}{6}}\)
\(=\dfrac{1}{5}\cdot5\sqrt{2}-2\cdot4\sqrt{6}-\sqrt{2}+\dfrac{12}{\sqrt{6}}\)
\(=\sqrt{2}-\sqrt{2}+2\sqrt{6}-8\sqrt{6}\)
\(=-6\sqrt{6}\)
e) Ta có: \(\dfrac{1}{2}\sqrt{48}-2\sqrt{75}-\sqrt{27}+5\sqrt{1\dfrac{1}{3}}\)
\(=\dfrac{1}{2}\cdot4\sqrt{3}-2\cdot5\sqrt{3}-3\sqrt{3}+5\cdot\dfrac{2}{\sqrt{3}}\)
\(=2\sqrt{3}-10\sqrt{3}-3\sqrt{3}+\dfrac{10\sqrt{3}}{3}\)
\(=-11\sqrt{3}+\dfrac{10\sqrt{3}}{3}\)
\(=\dfrac{-33+10\sqrt{3}}{3}\)
f) Ta có: \(\sqrt{150}+\sqrt{96}+\dfrac{9}{2}\cdot\sqrt{2\dfrac{2}{3}}-\sqrt{6}\)
\(=5\sqrt{6}+4\sqrt{6}+\dfrac{9}{2}\cdot\sqrt{\dfrac{8}{3}}-\sqrt{6}\)
\(=8\sqrt{6}+\dfrac{9}{2}\cdot\dfrac{2\sqrt{2}}{\sqrt{3}}\)
\(=8\sqrt{6}+3\sqrt{6}\)
\(=11\sqrt{6}\)
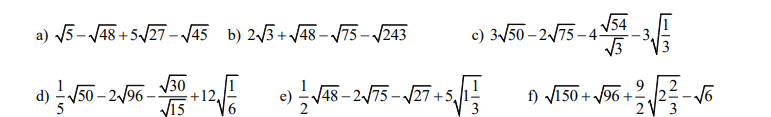



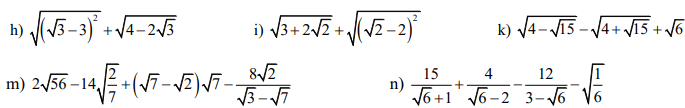
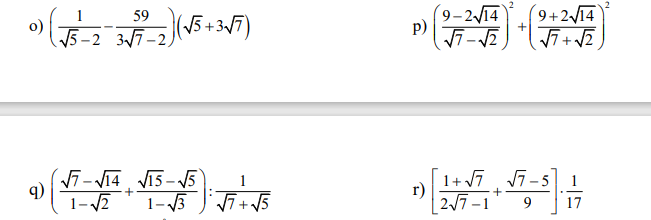

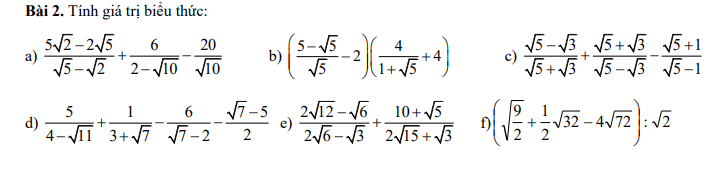
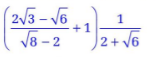

 với x ³ 0 và x ¹ 1.
với x ³ 0 và x ¹ 1.

 với x > 2017
với x > 2017