Nếu mọi nghiệm của phương trình f(x) = g(x) đều là nghiệm của phương trình f1(x) = g1(x) thì phương trình
f1(x) = g1(x) được gọi là phương trình hệ quả của phương trình f(x) = g(x).
Ta viết f(x) = g(x)  f1(x) = g1(x).
f1(x) = g1(x).
Ví dụ: Giải phương trình:
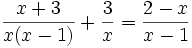 (4)
(4)
Giải
Điều kiện của phương trình (4) là x ≠ 0 và x ≠ 1.
Nhân hai vế của phương trình (4) với x(x - 1) ta được phương trình hệ quả:
(4)  x + 3 + 3(x - 1) = x(2 - x)
x + 3 + 3(x - 1) = x(2 - x)
 x2 + 2x = 0
x2 + 2x = 0
 x(x + 2) = 0.
x(x + 2) = 0.
Phương trình cuối cùng có hai nghiệm là x = 0 và x = -2.
Ta thấy x = 0 không thỏa mãn điều kiện của phương trình (4), đó là nghiệm ngoại lai, nên bị loại. Còn lại x = -2 thỏa mãn điều kiện và thỏa mãn phương trình (4).
Vậy phương trình (4) có nghiệm duy nhất là x = -2.
Nếu mọi nghiệm của phương trình \(f\left(x\right)=g\left(x\right)\) đều là nghiệm của phương trình \(f_1\left(x\right)=g_1\left(x\right)\)thì phương trình
\(f_1\left(x\right)=g_1\left(x\right)\) được gọi là phương trình hệ quả của phương trình \(f\left(x\right)=g\left(x\right)\)
