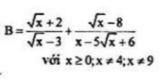\(P=\left(\dfrac{1}{a-1}+\dfrac{3\sqrt{a}+5}{a\sqrt{a}-a-\sqrt{a}+1}\right).\left(\dfrac{\left(\sqrt{a}+1\right)^2}{4\sqrt{a}}-1\right)\)
Ta có \(a\sqrt{a}-a-\sqrt{a}+1=\left(a-1\right)\left(\sqrt{a}-1\right)\)
ĐKXĐ: \(\left\{{}\begin{matrix}a-1\ne0\\\sqrt{a}-1>0\\a>0\end{matrix}\right.\) \(\Leftrightarrow a>1\)
\(P=\dfrac{\left(\sqrt{a}-1\right)+\left(3\sqrt{a}+5\right)}{\left(\sqrt{a}-1\right)\left(a-1\right)}.\dfrac{\left(a+2\sqrt{a}+1\right)-4\sqrt{a}}{4\sqrt{a}}\)
\(=\dfrac{4\sqrt{a}+4}{\left(\sqrt{a}-1\right)\left(a-1\right)}.\dfrac{a-2\sqrt{a}+1}{4\sqrt{a}}\) \(=\dfrac{4\left(\sqrt{a}-1\right)}{\left(\sqrt{a}-1\right)\left(a-1\right)}.\dfrac{\left(\sqrt{a}-1\right)^2}{4\sqrt{a}}\)
\(=\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}{a-1}=\dfrac{a-1}{a-1}=1\)
Ta có: \(P=\left(\dfrac{1}{a-1}+\dfrac{3\sqrt{a}+5}{a\sqrt{a}-a-\sqrt{a}+1}\right)\cdot\left(\dfrac{\left(\sqrt{a}+1\right)^2}{4\sqrt{a}}-1\right)\)
\(=\dfrac{\sqrt{a}-1+3\sqrt{a}+5}{\left(\sqrt{a}-1\right)^2\cdot\left(\sqrt{a}+1\right)}\cdot\dfrac{a+2\sqrt{a}+1-4\sqrt{a}}{4\sqrt{a}}\)
\(=\dfrac{4\sqrt{a}+4}{\left(\sqrt{a}+1\right)}\cdot\dfrac{1}{4\sqrt{a}}\)
\(=\dfrac{4\left(\sqrt{a}+1\right)}{4\sqrt{a}\left(\sqrt{a}+1\right)}=\dfrac{1}{\sqrt{a}}\)



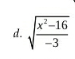 (tìm điều kiện xác định)
(tìm điều kiện xác định)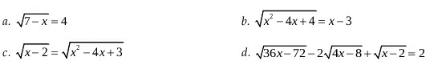 ( tìm x biết)
( tìm x biết)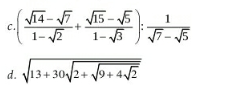 (rút gọn)
(rút gọn)