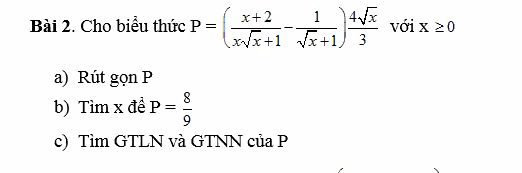Question

Phần c ạ, em cần ngay bây giờ ạ

Answer 1

\(P=\dfrac{4}{3}.\dfrac{\sqrt{x}}{x-\sqrt{x}+1}=\dfrac{4}{3}\left(1-\dfrac{x-2\sqrt{x}+1}{x-\sqrt{x}+1}\right)=\dfrac{4}{3}-\dfrac{4}{3}.\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+1}\le\dfrac{4}{3}\)

\(P_{max}=\dfrac{4}{3}\) khi \(x=1\)

Do \(\left\{{}\begin{matrix}\sqrt{x}\ge0\\x-\sqrt{x}+1=\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\end{matrix}\right.\) \(\Rightarrow P\ge0\)

\(P_{min}=0\) khi \(x=0\)

Answer 2

a: Ta có: \(P=\left(\dfrac{x+2}{x\sqrt{x}+1}-\dfrac{1}{\sqrt{x}+1}\right)\cdot\dfrac{4\sqrt{x}}{3}\)

\(=\dfrac{x+2-x+\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\cdot\dfrac{4\sqrt{x}}{3}\)

\(=\dfrac{4\sqrt{x}}{3x-3\sqrt{x}+3}\)