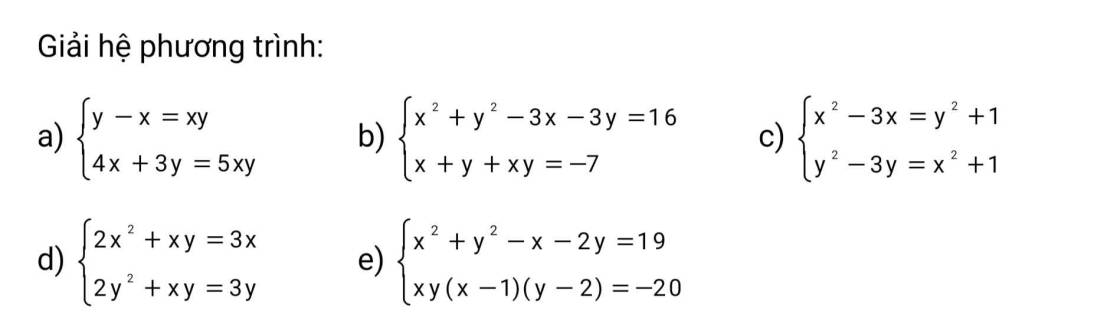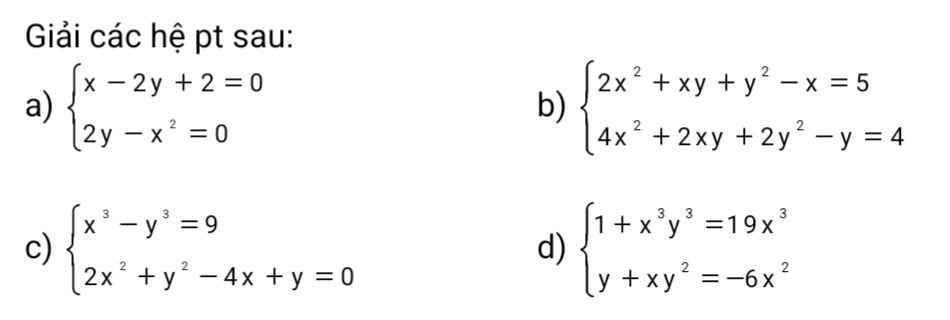a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
Xét tứ giác IHBM có \(\widehat{IHB}+\widehat{IMB}=90^0+90^0=180^0\)
nên IHBM là tứ giác nội tiếp
b: Ta có: IN\(\perp\)CH
AB\(\perp\)CH
Do đó: IN//AB
=>\(\widehat{CNI}=\widehat{CBA}\)
Xét (O) có
\(\widehat{CBA}\) là góc nội tiếp chắn cung CA
\(\widehat{CMA}\) là góc nội tiếp chắn cung CA
Do đó: \(\widehat{CBA}=\widehat{CMA}\)
=>\(\widehat{CNI}=\widehat{CMA}=\widehat{CMI}\)
=>CINM là tứ giác nội tiếp
=>\(\widehat{ICN}=\widehat{IMN}\)
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
ta có: \(\widehat{ICN}+\widehat{ACH}=\widehat{ACB}=90^0\)
\(\widehat{NMB}+\widehat{AMN}=\widehat{AMB}=90^0\)
mà \(\widehat{ICN}=\widehat{AMN}\)
nên \(\widehat{ACH}=\widehat{NMB}\)



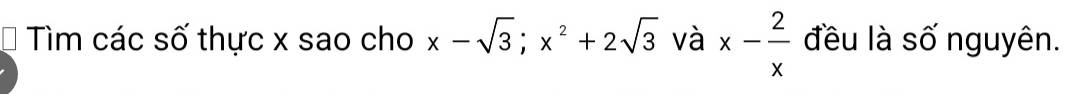 nhờ mọi người giúp vs ạ.
nhờ mọi người giúp vs ạ.

 mọi người giúp mik bài 4 câu a vs ạ
mọi người giúp mik bài 4 câu a vs ạ