t: \(\dfrac{sinx}{sinx+cosx}-\dfrac{cosx}{cosx-sinx}\)
\(=\dfrac{sinx}{sinx+cosx}+\dfrac{cosx}{sinx-cosx}\)
\(=\dfrac{sinx\left(sinx-cosx\right)+cosx\left(sinx+cosx\right)}{sin^2x-cos^2x}\)
\(=\dfrac{sin^2x+cos^2x}{sin^2x-cos^2x}=\dfrac{\dfrac{sin^2x}{sin^2x}+\dfrac{cos^2x}{sin^2x}}{\dfrac{sin^2x}{sin^2x}-\dfrac{cos^2x}{sin^2x}}=\dfrac{1+cot^2x}{1-cot^2x}\)
s: \(cos^3x\cdot\left(tan^3x+tan^2x+tanx+1\right)\)
\(=cos^3x\left[tan^2x\left(tanx+1\right)+\left(tanx+1\right)\right]\)
\(=cos^3x\left(tan^2x+1\right)\left(tanx+1\right)\)
\(=\dfrac{cos^3x}{cos^2x}\cdot\left(tanx+1\right)=cosx\cdot\left(tanx+1\right)\)
\(=cosx\cdot\left(\dfrac{sinx}{cosx}+1\right)=cosx\cdot\dfrac{sinx+cosx}{cosx}=sinx+cosx\)
=>\(\dfrac{sinx+cosx}{cos^3x}=tan^3x+tan^2x+tanx+1\)
q: \(\dfrac{1+tan^2x}{1-tan^2x}\)
\(=\dfrac{1+\left(\dfrac{sinx}{cosx}\right)^2}{1-\left(\dfrac{sinx}{cosx}\right)^2}=\dfrac{cos^2x+sin^2x}{cos^2x}:\dfrac{cos^2x-sin^2x}{cos^2x}\)
\(=\dfrac{1}{cos^2x}\cdot\dfrac{cos^2x}{cos^2x-sin^2x}=\dfrac{1}{cos^2x-sin^2x}\)
r: \(\left(sinx+cosx-1\right)\left(sinx-cosx+1\right)\)
\(=sin^2x-\left(cosx-1\right)^2\)
\(=sin^2x-\left(cos^2x-2\cdot cosx+1\right)\)
\(=sin^2x-cos^2x+2\cdot cosx-1\)
\(=sin^2x-cos^2x+2\cdot cosx-sin^2x-cos^2x\)
\(=2\cdot cosx-2\cdot cos^2x=2\cdot cosx\left(1-cosx\right)\)
=>\(\dfrac{sinx+cosx-1}{1-cosx}=\dfrac{2\cdot cosx}{sinx-cosx+1}\)
m: \(\dfrac{1+2\cdot sinx\cdot cosx}{sin^2x-cos^2x}\)
\(=\dfrac{sin^2x+cos^2x+2\cdot sinx\cdot cosx}{\left(sinx-cosx\right)\left(sinx+cosx\right)}\)
\(=\dfrac{\left(sinx+cosx\right)^2}{\left(sinx-cosx\right)\left(sinx+cosx\right)}=\dfrac{sinx+cosx}{sinx-cosx}\)
\(=\dfrac{\dfrac{sinx}{cosx}+\dfrac{cosx}{cosx}}{\dfrac{sinx}{cosx}-\dfrac{cosx}{cosx}}=\dfrac{tanx+1}{tanx-1}\)
n: \(\left(tan^2x-cot^2x\right)\cdot\left(sin^2x\cdot cos^2x\right)\)
\(=\left(\dfrac{sin^2x}{cos^2x}-\dfrac{cos^2x}{sin^2x}\right)\cdot\left(sin^2x\cdot cos^2x\right)\)
\(=\dfrac{sin^4x-cos^4x}{cos^2x\cdot sin^2x}\cdot sin^2x\cdot cos^2x=sin^4x-cos^4x\)
\(=\left(sin^2x+cos^2x\right)\left(sin^2x-cos^2x\right)=sin^2x-cos^2x=1-2\cdot cos^2x\)
=>\(\dfrac{1-2\cdot cos^2x}{sin^2x\cdot cos^2x}=tan^2x-cot^2x\)
o: \(\dfrac{cosx}{1+sinx}-\dfrac{1}{cosx}=\dfrac{cos^2x-\left(1+sinx\right)}{cosx\cdot\left(1+sinx\right)}\)
\(=\dfrac{1-sin^2x-1-sinx}{cosx\left(1+sinx\right)}=\dfrac{-sinx\cdot\left(sinx+1\right)}{cosx\left(1+sinx\right)}\)
\(=-\dfrac{sinx}{cosx}=-tanx\)
=>\(\dfrac{cosx}{1+sinx}+tanx=\dfrac{1}{cosx}\)
p: \(\dfrac{tan^2x-tan^2y}{tan^2x\cdot tan^2y}=\dfrac{\left(\dfrac{sinx}{cosx}\right)^2-\left(\dfrac{siny}{cosy}\right)^2}{\dfrac{sin^2x}{cos^2x}\cdot\dfrac{sin^2y}{cos^2y}}\)
\(=\dfrac{sin^2x\cdot cos^2y-sin^2y\cdot cos^2x}{cos^2x\cdot cos^2y}:\dfrac{sin^2x\cdot sin^2y}{cos^2\cdot cos^2y}\)
\(=\dfrac{sin^2x\cdot cos^2y-sin^2y\cdot cos^2x}{sin^2x\cdot sin^2y}\)
\(=\dfrac{sin^2x\left(1-sin^2y\right)-sin^2y\left(1-sin^2x\right)}{sin^2x\cdot sin^2y}=\dfrac{sin^2x-sin^2x\cdot sin^2y-sin^2y+sin^2x\cdot sin^2y}{sin^2x\cdot sin^2y}=\dfrac{sin^2x-sin^2y}{sin^2x\cdot sin^2y}\)

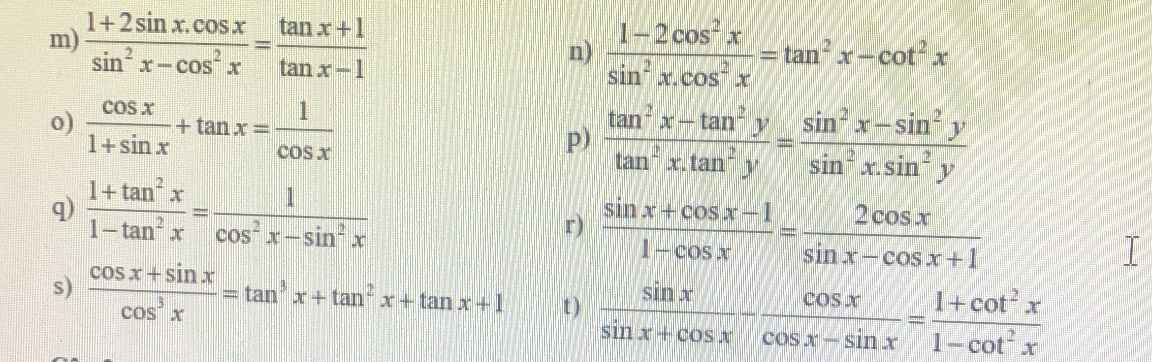




 mọi người giúp em với em cảm ơn nhiều lắmmmmm
mọi người giúp em với em cảm ơn nhiều lắmmmmm






