\(\left(ab+bc+ca\right)^2\ge3abc\left(a+b+c\right)\Rightarrow\dfrac{ab+bc+ca}{abc}\ge\dfrac{3\left(a+b+c\right)}{ab+bc+ca}\)
\(\Rightarrow a+b+c\ge\dfrac{1}{16}\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)=\dfrac{1}{16}\left(\dfrac{ab+bc+ca}{abc}\right)\ge\dfrac{3}{16}\left(\dfrac{a+b+c}{ab+bc+ca}\right)\)
\(\Rightarrow ab+bc+ca\ge\dfrac{3}{16}\)
Ta có:
\(a+b+\sqrt{2\left(a+c\right)}=a+b+\sqrt{\dfrac{a+c}{2}}+\sqrt{\dfrac{a+c}{2}}\ge3\sqrt[3]{\dfrac{\left(a+b\right)\left(a+c\right)}{2}}\)
\(\Rightarrow\left(\dfrac{1}{a+b+\sqrt{2\left(a+c\right)}}\right)^3\le\dfrac{2}{27\left(a+b\right)\left(a+c\right)}\)
Tương tự và cộng lại:
\(P\le\dfrac{2}{27}\left(\dfrac{1}{\left(a+b\right)\left(a+c\right)}+\dfrac{1}{\left(a+b\right)\left(b+c\right)}+\dfrac{1}{\left(a+c\right)\left(b+c\right)}\right)\)
\(P\le\dfrac{4}{27}.\dfrac{a+b+c}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\)
Mặt khác:
\(\left(a+b\right)\left(b+c\right)\left(c+a\right)=\left(a+b+c\right)\left(ab+bc+ca\right)-abc\)
\(=\left(a+b+c\right)\left(ab+bc+ca\right)-\sqrt[3]{abc}.\sqrt[3]{ab.bc.ca}\)
\(\ge\left(a+b+c\right)\left(ab+bc+ca\right)-\dfrac{1}{3}.\left(a+b+c\right).\dfrac{1}{3}\left(ab+bc+ca\right)\)
\(=\dfrac{8}{9}\left(a+b+c\right)\left(ab+bc+ca\right)\)
\(\Rightarrow P\le\dfrac{4}{27}.\dfrac{a+b+c}{\dfrac{8}{9}\left(a+b+c\right)\left(ab+bc+ca\right)}=\dfrac{1}{6\left(ab+bc+ca\right)}\le\dfrac{1}{6.\dfrac{3}{16}}=\dfrac{8}{9}\)
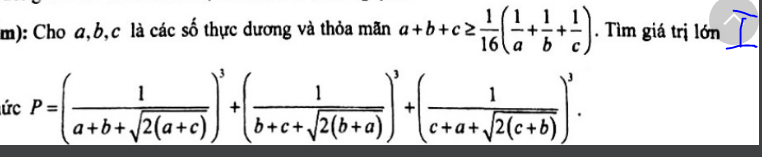 mọi người giúp em với em cảm ơn nhiều lắmmmmm
mọi người giúp em với em cảm ơn nhiều lắmmmmm













