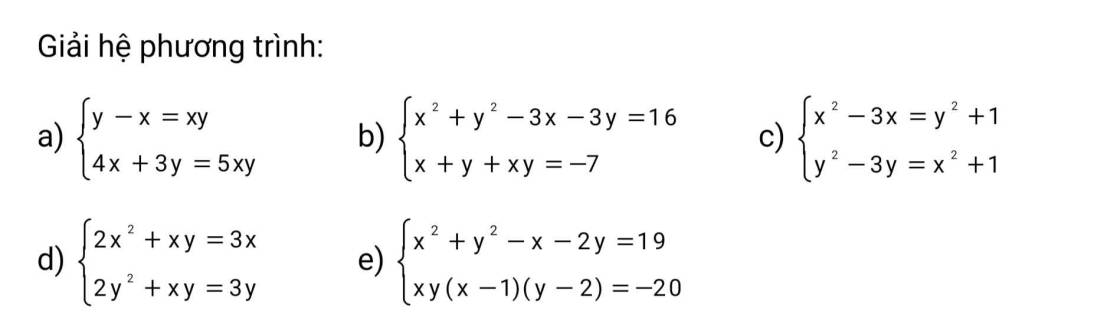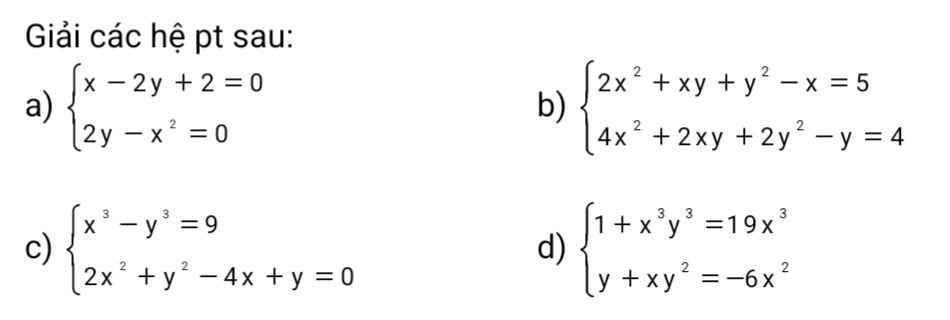a:Xét ΔOHB vuông tại H có HM là đường cao
nên \(OM\cdot OB=OH^2\left(1\right)\)
Xét ΔOHC vuông tại H có HN là đường cao
nên \(ON\cdot OC=OH^2\left(2\right)\)
Từ (1) và (2) suy ra \(OM\cdot OB=ON\cdot OC\)
\(OM\cdot OB=OH^2\)
=>\(OM\cdot OB=OA^2\)
=>\(\dfrac{OM}{OA}=\dfrac{OA}{OB}\)
Xét ΔOMA và ΔOAB có
\(\dfrac{OM}{OA}=\dfrac{OA}{OB}\)
\(\widehat{MOA}\) chung
Do đó: ΔOMA đồng dạng với ΔOAB
=>\(\widehat{MAO}=\widehat{OBA}\)
=>\(\widehat{MAO}=\widehat{MOA}\)
=>MO=MA
=>M nằm trên đường trung trực của AO
ON*OC=OA2
=>ON/OA=OA/OC
Xét ΔONA và ΔOAC có
\(\dfrac{ON}{OA}=\dfrac{OA}{OC}\)
\(\widehat{NOA}\) chung
Do đó: ΔONA đồng dạng với ΔOAC
=>\(\widehat{ONA}=\widehat{OAC}=\widehat{NAO}\)
=>\(\widehat{NAO}=\widehat{NOA}\)
=>NA=NO
=>N nằm trên đường trung trực của AO
=>MN là đường trung trực của AO
=>MN luôn đi qua O
b:
Gọi D là giao điểm của OA và MN
=>OA\(\perp\)MN tại D
\(OM\cdot OB=ON\cdot OC\)
=>\(\dfrac{OM}{ON}=\dfrac{OC}{OB}\)
=>\(\dfrac{OM}{OC}=\dfrac{ON}{OB}\)
Xét ΔOMN và ΔOCB có
\(\dfrac{OM}{OC}=\dfrac{ON}{OB}\)
\(\widehat{MON}\) chung
Do đó: ΔOMN đồng dạng với ΔOCB
OH\(\perp\)BC
OD\(\perp\)MN
=>\(\dfrac{OM}{OD}=\dfrac{OC}{OH}\)
=>\(\dfrac{OM}{\dfrac{R}{2}}=\dfrac{OC}{R}\)
=>\(OM=\dfrac{1}{2}OC\)
\(OM\cdot OB=OH^2\)
=>\(\dfrac{1}{2}\cdot OC\cdot OB=R^2\)
=>\(OB\cdot OC=2R^2\)