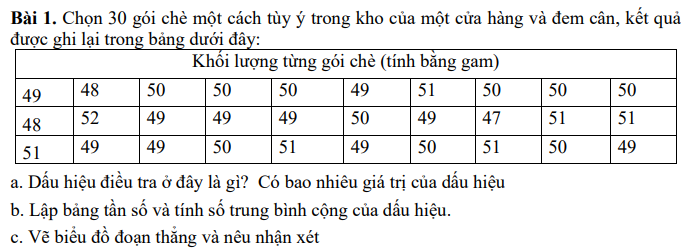
\(\dfrac{7}{6}=1+\dfrac{1}{6};1,25=1+\dfrac{1}{4}\)
mà \(\dfrac{1}{6}< \dfrac{1}{4}\)
nên \(\dfrac{7}{6}< 1.25\)
mà \(1,25< 3,5< 5\sqrt{30}=\sqrt{750}\)
nên \(\dfrac{7}{6}< 1,25< 3,5< \sqrt{750}\)(1)
Ta có: \(\dfrac{1}{2}=1-\dfrac{1}{2};\dfrac{6}{7}=1-\dfrac{1}{7}\)
Ta có: 2<7
=>\(\dfrac{1}{2}>\dfrac{1}{7}\)
=>\(-\dfrac{1}{2}< -\dfrac{1}{7}\)
=>\(1-\dfrac{1}{2}< 1-\dfrac{1}{7}\)
=>\(\dfrac{1}{2}< \dfrac{6}{7}< 1< \dfrac{7}{6}\left(2\right)\)
\(-\dfrac{88}{101}>-1;-1>-1\dfrac{1}{2}\)
Do đó: \(-1\dfrac{1}{2}< -\dfrac{88}{101}< 0< \dfrac{1}{2}\left(3\right)\)
Từ (1),(2),(3) suy ra \(-1\dfrac{1}{2}< -\dfrac{88}{101}< \dfrac{1}{2}< \dfrac{6}{7}< \dfrac{7}{6}< 1,25< 3,5< \sqrt{750}\)

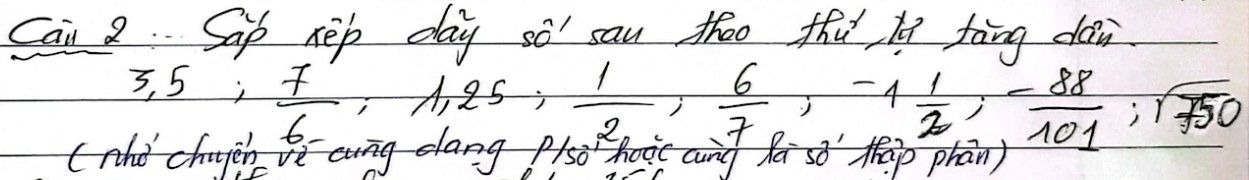


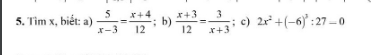

 giúp em với ạ e, đang cần gấp lắm ạ
giúp em với ạ e, đang cần gấp lắm ạ
 mng ơi giúp em với ạ! e đag cần gấp! e cảm ơn mng nhiều lắmm <33
mng ơi giúp em với ạ! e đag cần gấp! e cảm ơn mng nhiều lắmm <33 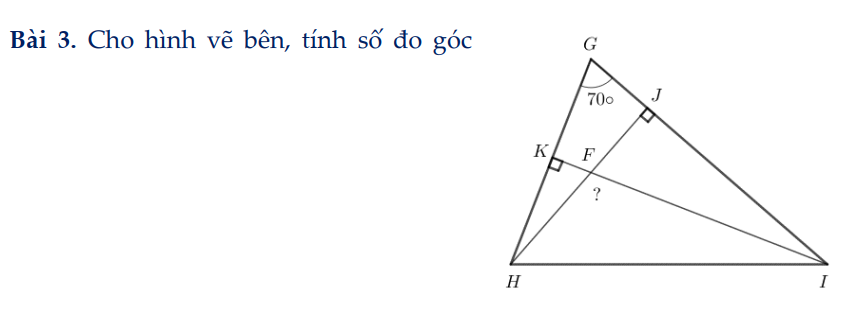 cần gấp
cần gấp