Bài 7: Trường hợp đồng dạng thứ ba
Các câu hỏi tương tự
Cho hình bình hành ABCD, điểm F trên cạnh BC. Tia AF cắt BD và DC lần lượt ở E và G. Chứng minh. a) ∆BEF~∆DEA; ∆DGE~∆BAE. b) AE^2 = EF~EG
Cho tam giác ABC nhọn (AB<AC) có hai đường cao BE,CF cắt nhau tại H. Chứng minh rằng: a) AF . AB = AE . AC; b) HB . HE = HF . HC; c) BF . BA = BH . BE; d) CH . CF = CE . CA; e) EB . EH = EA . EC; f) FC . FH = FA . FB. Xin hãy giúp mình với ạ. Xin cảm ơn!
Cho HBH ABCD có đg chéo AC BD . Gọi I , K lần lượt là hình chiếu của điểm B,D trên đg thẳng AC. Gọi hình chiếu của điểm C trên dt AB , AD lần lượt là H, K.
a) CM : BJ DI
b)CM AH . AD + AD . AK EF.EG
c) Qua điểm A kẻ đt d bất kỳ cắt đg chéo BD, cạnh Bc và tia Dc lần lượt tại E,F,G.CM AE2 EF.EG
d) Cm dfrac{1}{AE} dfrac{1}{AF}+ dfrac{1}{AG}
e) Cm khi đg thẳng d thay đổi quanh điểm A thì tích BD.DG ko đổi
Đọc tiếp
Cho HBH ABCD có đg chéo AC > BD . Gọi I , K lần lượt là hình chiếu của điểm B,D trên đg thẳng AC. Gọi hình chiếu của điểm C trên dt AB , AD lần lượt là H, K.
a) CM : BJ = DI
b)CM AH . AD + AD . AK = EF.EG
c) Qua điểm A kẻ đt d bất kỳ cắt đg chéo BD, cạnh Bc và tia Dc lần lượt tại E,F,G.CM AE2= EF.EG
d) Cm \(\dfrac{1}{AE}\)= \(\dfrac{1}{AF}\)+ \(\dfrac{1}{AG}\)
e) Cm khi đg thẳng d thay đổi quanh điểm A thì tích BD.DG ko đổi
Cho tam giác ABC, trung tuyến AM. Qua điểm D thuộc cạnh BC, vẽđường thẳng song song với AM, cắt AB, AC tại E và F
a)Chứng minh DE + DF không đổi khi D di động trên BC
b) Qua A vẽ đường thẳng song song với BC, cắt FE tại K. Chứng minh rằng K là trung điểm của FE
cho hình thang ABCD , có đáy nhỏ là AB (AB//CD) , AB= 3cm : AD= 4cm ; BD= 6cm và góc DAB= góc DBC . đường chéo AC và BD cắt tại O , qua B kẻ đường thẳng // với AD , đường này cắt AC ở F và cắt CD ở E
a) cm tam giác ABD đồng dạng tam giác BDC
b) tính độ dài BC, CD
C) tính tỉ số giữa cgu vi tam giác BOF và tam giác DOA
Cho hình bình hành ABCD (h.46) có độ dài các cạnh AB 12cm, BC 7cm. Trên cạnh AB lấy một điểm E sao cho AE 8cm. Đường thẳng DE cắt cạnh CB kéo dài tại F
a) Trong hình vẽ đã cho có bao nhiêu cặp tam giác đồng dạng với nhau ? Hãy viết các cặp tam giác đồng dạng với nhau theo các đỉnh tương ứng ?
b) Tính độ dài các đoạn thẳng EF và BF, biết rằng DE 10 cm
Đọc tiếp
Cho hình bình hành ABCD (h.46) có độ dài các cạnh AB = 12cm, BC = 7cm. Trên cạnh AB lấy một điểm E sao cho AE = 8cm. Đường thẳng DE cắt cạnh CB kéo dài tại F
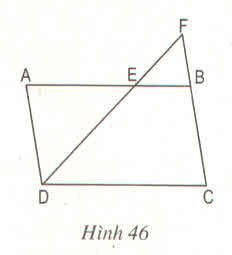
a) Trong hình vẽ đã cho có bao nhiêu cặp tam giác đồng dạng với nhau ? Hãy viết các cặp tam giác đồng dạng với nhau theo các đỉnh tương ứng ?
b) Tính độ dài các đoạn thẳng EF và BF, biết rằng DE = 10 cm
Cho hình chữ nhật ABCD có AB=12cm, BC=9cm. GỌi H là chân đường vuông góc kẻ từ S xuống Bd. Tia AH cắt DC tại F và cắt đường thẳng BC tại E. Chứng minh AH2 = EH . FH
Cho hình thoi ABCD có góc A bằng 600. Qua C kẻ đường thẳng d không cắt hình thoi nhưng cắt
đường thẳng AB tại E và đường thẳng AD tại F.
a)Chứng minh : tam giác BEC đồng dạng tam giác AEF
b)Chứng minh : tam giác DCF đồng dạng tam giác AEF
c)Chứng minh : BE.DF = DB2.
d) Chứng minh : tam giác BDE đồng dạng tam giác DBF
Cho ∆𝐴𝐵𝐶 vuông tại A. Tia phân giác góc B cắt AC tại D. Kẻ CE vuông góc với đường thẳng BD tại E.
a) Chứng minh ∆𝐴𝐵𝐷 đồng dạng với ∆𝐷𝐶𝐸 suy ra 𝐷𝐴.𝐷𝐶=𝐷𝐸.𝐷𝐵
b) Chứng minh 𝐸𝐴𝐷̂=𝐸𝐵𝐶̂
Cho tam giác ABC, trung tuyến BI, CQ. Qua D kẻ đường thẳng // CQ cắt AB và BG theo thứ tự tại E và H. Qua D kẻ đường thẳng // BI cắt AC và CG theo thứ tự tại F và K, EF cắt BI và CQ theo thứ tự ở M và N. Chứng minh:
a, EM = MN = NF.
b, DG đi qua trung điểm MN.
c, \(S_1\le\dfrac{1}{6}S\) (S1 và S lần lượt là diện tích tứ giác DHGK và tam giác ABC).
