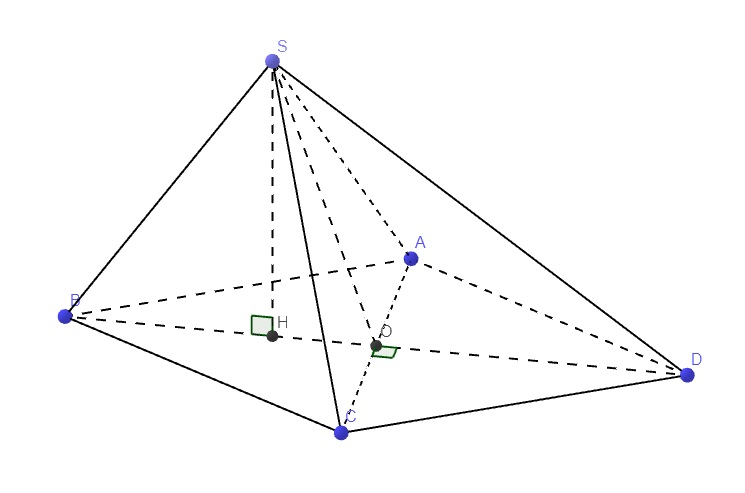
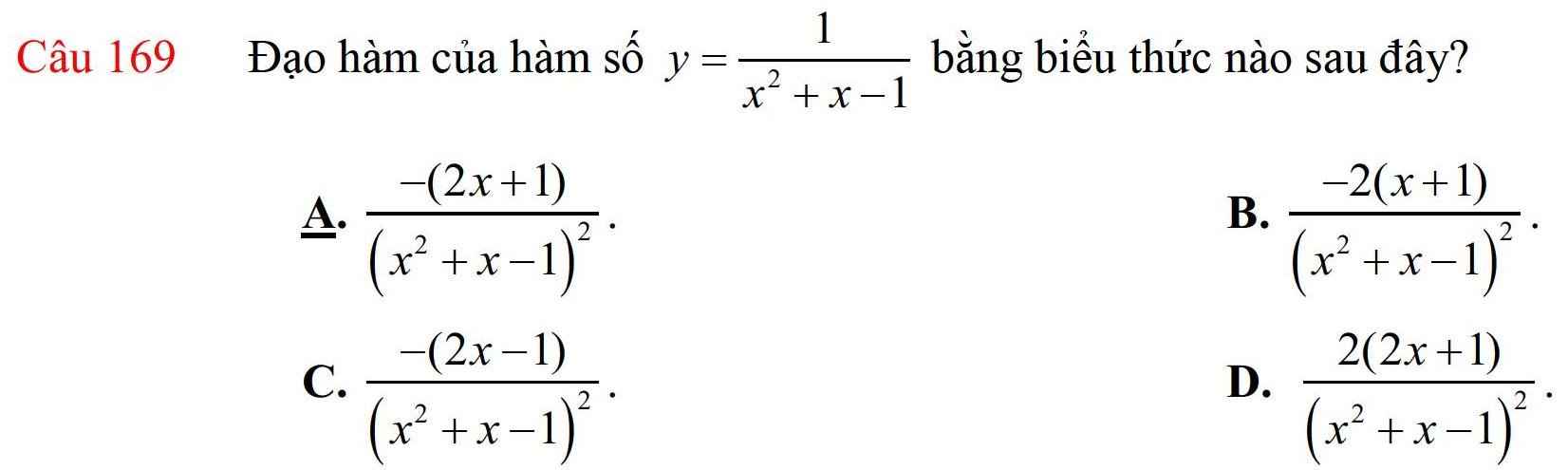Gọi O là giao điểm AC và BD \(\Rightarrow H\in BO\Rightarrow H\in BD\) do tam giác ABC đều
\(\Rightarrow SH\in\left(SBD\right)\)
Ta có: \(\left\{{}\begin{matrix}AC\perp BD\left(\text{2 đường chéo hình thoi}\right)\\SH\perp\left(ABCD\right)\Rightarrow SH\perp AC\end{matrix}\right.\)
\(\Rightarrow AC\perp\left(SBD\right)\)
b.
\(SH\perp\left(ABCD\right)\Rightarrow SH\) là hình chiếu vuông góc của SB lên (ABCD)
\(\Rightarrow\widehat{SBH}\) là góc giữa SB và (ABCD)
\(BH=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\Rightarrow tan\widehat{SBH}=\dfrac{SH}{BH}=\sqrt{6}\) \(\Rightarrow\widehat{SBH}\approx67^048'\)
Theo cm câu a ta có \(AC\perp\left(SBD\right)\) tại O
\(\Rightarrow SO\) là hình chiếu vuông góc của SC lên (SBD)
\(\Rightarrow\widehat{CSO}\) là góc giữa SC và (SBD)
\(OC=\dfrac{1}{2}AC=\dfrac{a}{2}\)
\(OH=\dfrac{1}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{6}\Rightarrow SO=\sqrt{SH^2+OH^2}=\dfrac{5a\sqrt{3}}{6}\)
\(\Rightarrow tan\widehat{CSO}=\dfrac{OC}{SO}=\dfrac{\sqrt{3}}{5}\Rightarrow\widehat{CSO}\approx19^0\)
 làm hộ em bài 3Nhãn
làm hộ em bài 3Nhãn



 Giải bài này hộ mình với!!!
Giải bài này hộ mình với!!!