18b:
a: ĐKXĐ: \(\left\{{}\begin{matrix}x+5>=0\\x>=0\end{matrix}\right.\Leftrightarrow x>=0\)
\(\sqrt{x+5}=1+\sqrt{x}\)
=>\(\left(\sqrt{x+5}\right)^2=\left(1+\sqrt{x}\right)^2\)
=>\(x+2\sqrt{x}+1=x+5\)
=>\(2\sqrt{x}=4\)
=>\(\sqrt{x}=2\)
=>x=4(nhận)
b: ĐKXĐ: 2x+1>=0
=>\(x>=-\dfrac{1}{2}\)
\(5\sqrt{2x+1}+\dfrac{7}{3}\sqrt{18x+9}-\sqrt{8x+4}-\sqrt{2x+1}=18\)
=>\(4\sqrt{2x+1}+\dfrac{7}{3}\cdot3\sqrt{2x+1}-2\sqrt{2x+1}=18\)
=>\(9\sqrt{2x+1}=18\)
=>\(2x+1=4\)
=>\(x=\dfrac{3}{2}\left(nhận\right)\)
a:
ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\3x-2>=0\end{matrix}\right.\Leftrightarrow x>=\dfrac{2}{3}\)
\(\sqrt{x}+\sqrt{3x-2}=2\)
=>\(\left(\sqrt{x}+\sqrt{3x-2}\right)^2=4\)
=>\(x+3x-2+2\sqrt{x\left(3x-2\right)}=4\)
=>\(4x-2+2\sqrt{x\left(3x-2\right)}=4\)
=>\(2\sqrt{x\left(3x-2\right)}=4x-6\)
=>\(\sqrt{3x^2-2x}=2x-3\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{3}{2}\\3x^2-2x=4x^2-12x+9\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{3}{2}\\4x^2-12x+9-3x^2+2x=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{3}{2}\\x^2-10x+9=0\end{matrix}\right.\Leftrightarrow x=9\)
b: ĐKXĐ: x+1>=0
=>x>=-1
\(2\sqrt{9x+9}-\dfrac{1}{4}\sqrt{16x+16}-5\sqrt{x+1}=-6-\sqrt{4x+4}\)
=>\(6\sqrt{x+1}-\dfrac{1}{4}\cdot4\sqrt{x+1}-5\sqrt{x+1}+\sqrt{4x+4}=-6\)
=>\(6\sqrt{x+1}-\sqrt{x+1}-5\sqrt{x+1}+2\sqrt{x+1}=-6\)
=>\(2\sqrt{x+1}=-6\)(vô lý)
Vậy: Phương trình vô nghiệm








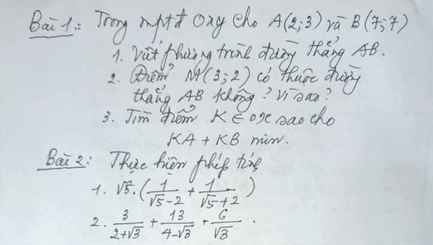 làm hộ mik bài 1 thôi nha
làm hộ mik bài 1 thôi nha