a: Xét tứ giác HABF có \(\widehat{HAB}+\widehat{HFB}=90^0+90^0=180^0\)
nên HABF là tứ giác nội tiếp
=>H,A,B,F cùng thuộc một đường tròn
b: Xét ΔCFH vuông tại F và ΔCAB vuông tại A có
\(\widehat{FCH}\) chung
Do đó: ΔCFH~ΔCAB
=>\(\dfrac{CF}{CA}=\dfrac{CH}{CB}\)
=>\(\dfrac{CF}{CH}=\dfrac{CA}{CB}\)
=>\(CF\cdot CB=CH\cdot CA\)
Xét ΔCFA và ΔCHB có
\(\dfrac{CF}{CH}=\dfrac{CA}{CB}\)
\(\widehat{FCA}\) chung
Do đó: ΔCFA~ΔCHB
=>\(\widehat{CAF}=\widehat{CBH}\)
c: Xét ΔCKB có
CA,KF là các đường cao
CA cắt KF tại H
Do đó: H là trực tâm của ΔCKB
=>BH\(\perp\)CK tại E
Xét ΔCEH vuông tại E và ΔCAK vuông tại A có
\(\widehat{ECH}\) chung
Do đó: ΔCEH~ΔCAK
=>\(\dfrac{CE}{CA}=\dfrac{CH}{CK}\)
=>\(\dfrac{CE}{CH}=\dfrac{CA}{CK}\)
Xét ΔCEA và ΔCHK có
\(\dfrac{CE}{CH}=\dfrac{CA}{CK}\)
\(\widehat{ECA}\) chung
Do đó: ΔCEA~ΔCHK
=>\(\widehat{CAE}=\widehat{CKH}\)
mà \(\widehat{CAF}=\widehat{CBH}\) và \(\widehat{CKH}=\widehat{CBH}\left(=90^0-\widehat{ECB}\right)\)
nên \(\widehat{CAE}=\widehat{CAF}\)
=>AC là phân giác của góc EAF
 helpppp
helpppp


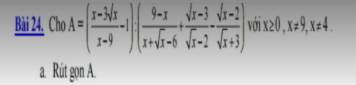 helpppp
helpppp
