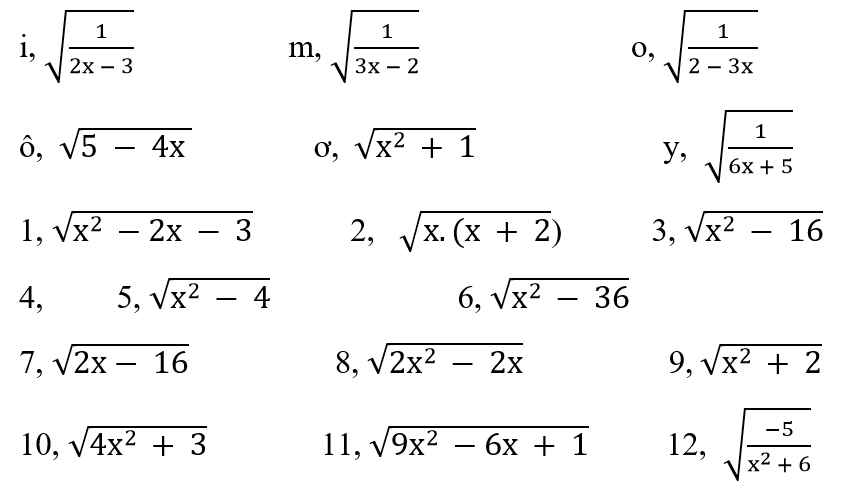a: Xét tứ giác BNMC có
\(\widehat{BNC}=\widehat{BMC}=90^0\)
nên BNMC là tứ giác nội tiếp
Xét ΔABC có
BM,CN là các đường cao
BM cắt CN tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC
b: Kẻ tiếp tuyến Ax của (O)
Xét (O) có
\(\widehat{xAC}\)là góc tạo bởi tiếp tuyến Ax và dây cung AC
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{xAC}=\widehat{ABC}\)
mà \(\widehat{ABC}=\widehat{AMN}\left(=180^0-\widehat{NMC}\right)\)
nên \(\widehat{xAC}=\widehat{AMN}\)
mà hai góc này là hai góc ở vị trí so le trong
nên Ax//MN
Ta có: Ax//MN
AK\(\perp\)Ax
Do đó: AK\(\perp\)MN
Đúng 0
Bình luận (0)
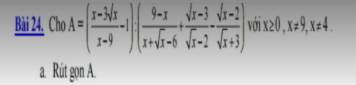helpppp
