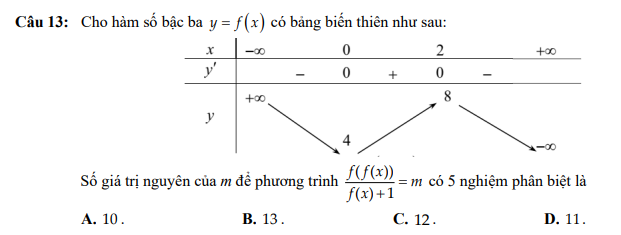
Nghịch suy ra \(f\left(x\right)=-x^3+3x^2+4\)
\(g\left(x\right)=\dfrac{f\left(f\left(x\right)\right)}{f\left(x\right)+1}\); \(g\left(u\right)=\dfrac{f\left(u\right)}{u+1}\)
\(g'\left(u\right)=u'.\dfrac{\left(u+1\right).f'\left(u\right)-f\left(u\right)}{\left(u+1\right)^2}=0\Rightarrow\left[{}\begin{matrix}u'=0\\\left(u+1\right)f'\left(u\right)-f\left(u\right)=0\left(2\right)\end{matrix}\right.\)
\(\left(2\right)\Leftrightarrow\left(u+1\right)\left(-3u^2+6u\right)-\left(-u^3+3u^2+4\right)=0\)
\(\Leftrightarrow-2\left(u-1\right)^2\left(u+2\right)=0\Rightarrow u=-2\)
Từ đồ thị ta thấy \(f\left(x\right)=-2\) có đúng 1 nghiệm \(x=a>2\)
\(f\left(-2\right)=24\Rightarrow g\left(a\right)=\dfrac{f\left(-2\right)}{-2+1}=-24\)
\(g\left(0\right)=\dfrac{f\left(4\right)}{4+1}=-2,4\); \(g\left(2\right)=\dfrac{f\left(8\right)}{8+1}=-35,11\)
Từ đồ thị thấy \(f\left(x\right)+1=0\Leftrightarrow f\left(x\right)=-1\) có nghiệm \(x=b\in\left(2;a\right)\)
BBT:
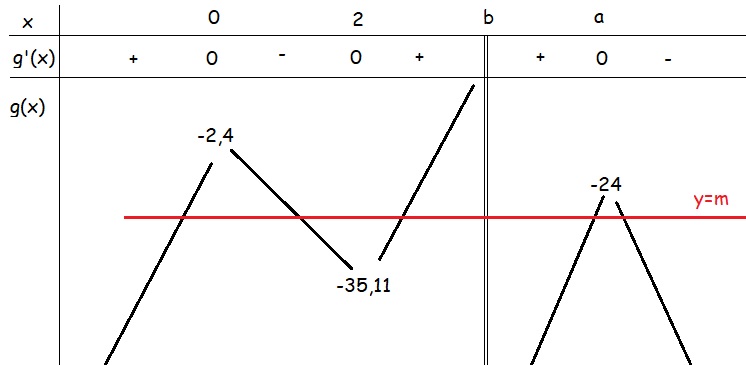
Từ BBT ta thấy \(-35,11< m< -24\)
Nên có 10 giá trị nguyên