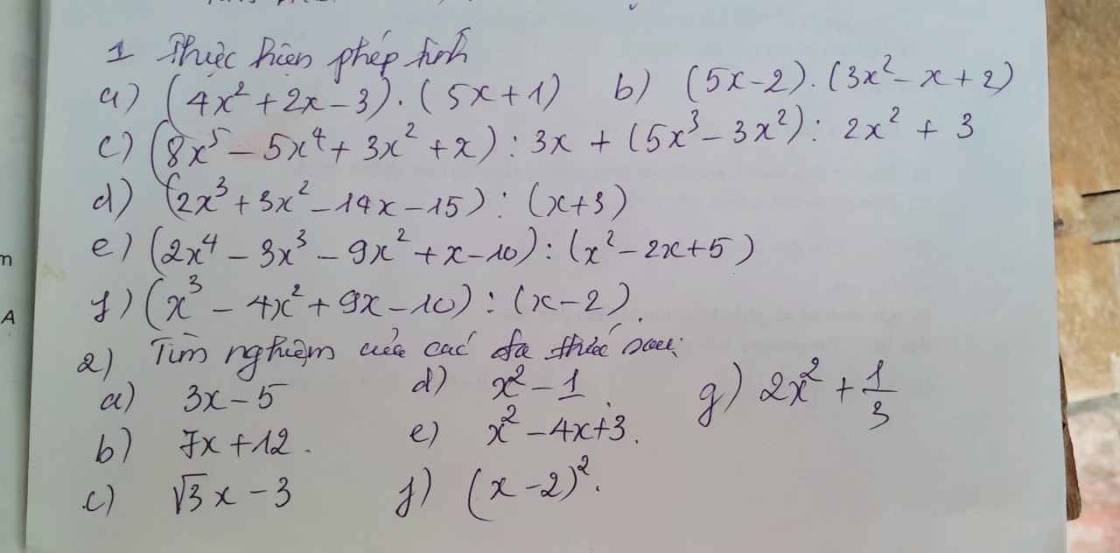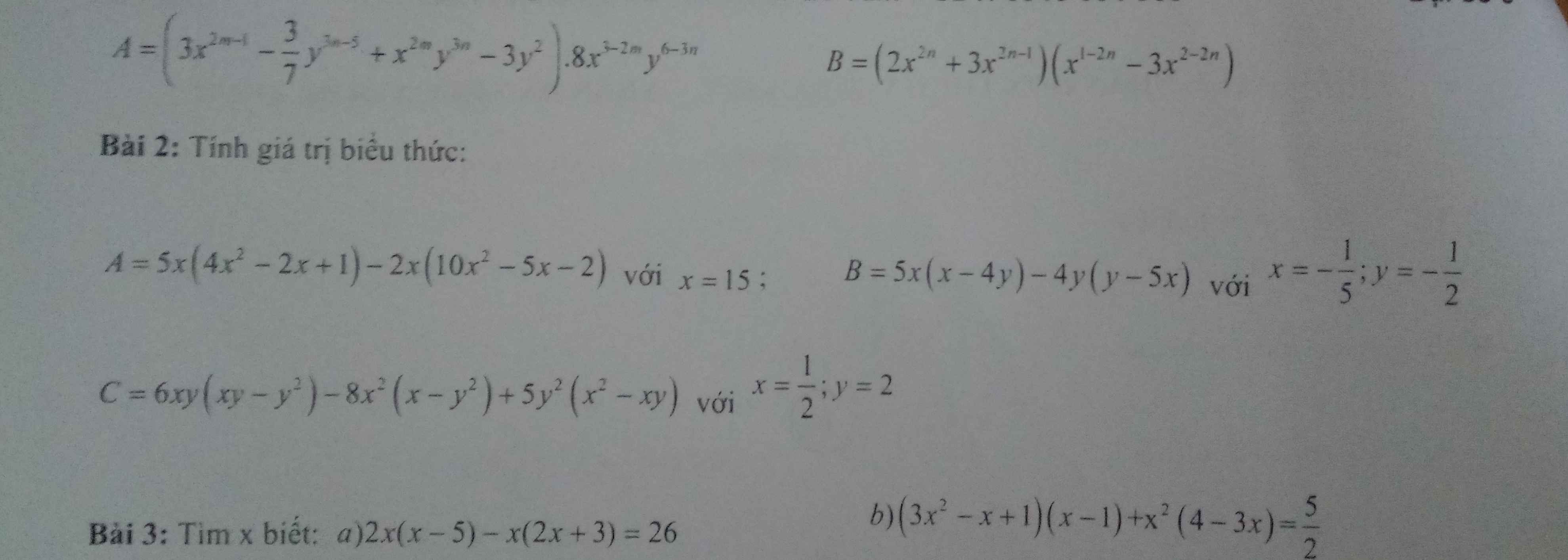Bài 2:
a) \(3x-5=0\)
\(\Rightarrow3x=5\)
\(\Rightarrow x=\dfrac{5}{3}\)
Vậy: \(x=\dfrac{5}{3}\)
b) \(7x+12=0\)
\(\Rightarrow7x=-12\)
\(\Rightarrow x=-\dfrac{12}{7}\)
Vậy: \(x=-\dfrac{12}{7}\)
c) \(\sqrt{3}x-3=0\)
\(\Rightarrow\sqrt{3}x=3\)
\(\Rightarrow x=\dfrac{3}{\sqrt{3}}\)
\(\Rightarrow x=\dfrac{\left(\sqrt{3}\right)^2}{\sqrt{3}}\)
\(\Rightarrow x=\sqrt{3}\)
Vậy: \(x=\sqrt{3}\)
d) \(x^2-1=0\)
\(\Rightarrow x^2=1\)
\(\Rightarrow x^2=\left(\pm1\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
Vậy: \(x=\pm1\)
e) \(x^2-4x+3=0\)
\(\Rightarrow x^2-x-3x+3=0\)
\(\Rightarrow x\left(x-1\right)-3\left(x-1\right)=0\)
\(\Rightarrow\left(x-1\right)\left(x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-1=0\\x-3=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)
Vậy: \(\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)
f) \(\left(x-2\right)^2=0\)
\(\Rightarrow\left(x-2\right)^2=0^2\)
\(\Rightarrow x-2=0\)
\(\Rightarrow x=2\)
Vậy: \(x=2\)
g) \(2x^2+\dfrac{1}{3}=0\)
Ta có: \(2x^2\ge0\forall x\)
\(\Rightarrow2x^2+\dfrac{1}{3}\ge\dfrac{1}{3}\forall x\)
Mà: \(\dfrac{1}{3}>0\)
\(\Rightarrow2x^2+\dfrac{1}{3}=0\) (vô lý)
Không có x thỏa mãn
2:
a: 3x-5=0
=>3x=5
=>x=5/3
b: 7x+12=0
=>7x=-12
=>x=-12/7
c: \(x\sqrt{3}-3=0\)
=>\(x\sqrt{3}=3\)
=>\(x=\sqrt{3}\)
d: x^2-1=0
=>(x-1)(x+1)=0
=>x-1=0 hoặc x+1=0
=>x=-1 hoặc x=1
e: x^2-4x+3=0
=>(x-1)(x-3)=0
=>x-1=0 hoặc x-3=0
=>x=1 hoặc x=3
f: (x-2)^2=0
=>x-2=0
=>x=2
g: 2x^2+1/3=0
=>2x^2=-1/3
=>x^2=-1/6(loạI)