a: \(\sin a=\sqrt{1-\left(\dfrac{5}{13}\right)^2}=\dfrac{12}{13}\)
\(\tan a=\dfrac{12}{5}\)
b: \(\sin a=\sqrt{1-\left(\dfrac{15}{17}\right)^2}=\dfrac{8}{17}\)
\(\tan a=\dfrac{8}{15}\)
c: \(\sin a=\sqrt{1-0.6^2}=0.8\)
nên \(\tan a=\dfrac{4}{3}\)
a: \(\sin a=\sqrt{1-\left(\dfrac{5}{13}\right)^2}=\dfrac{12}{13}\)
\(\tan a=\dfrac{12}{5}\)
b: \(\sin a=\sqrt{1-\left(\dfrac{15}{17}\right)^2}=\dfrac{8}{17}\)
\(\tan a=\dfrac{8}{15}\)
c: \(\sin a=\sqrt{1-0.6^2}=0.8\)
nên \(\tan a=\dfrac{4}{3}\)
chứng minh các biểu thức sau :
a) \(\dfrac{cos\alpha}{1-sin\alpha}=\dfrac{1+sin\alpha}{cos\alpha}\)
b) \(\dfrac{\left(sin\alpha+cos\alpha\right)^2-\left(sin\alpha-cos\alpha\right)^2}{sin\alpha+cos\alpha}\)
Hãy đơn giản biểu thức :
a) \(1-\sin^2\alpha\)
b) \(\sin^4\alpha+\cos^4\alpha+2\sin^2\alpha\cos^2\alpha\)
c) \(\left(1-\cos\alpha\right)\left(1+\cos\alpha\right)\)
d) \(tg^2\alpha-\sin^2\alpha.tg^2\alpha\)
e) \(1+\sin^2\alpha+\cos^2\alpha\)
g) \(\cos^2\alpha+tg^2\alpha.\cos^2\alpha\)
h) \(\sin\alpha-\sin\alpha.\cos^2\alpha\)
i) \(tg^2\alpha\left(2\cos^2\alpha+\sin^2\alpha-1\right)\)
1. Cho cotg\(\alpha\)=5. Tính giá trị của biểu thức : \(\dfrac{\sin\alpha+\cos\alpha}{\sin\alpha-\cos\alpha}\)
2. Cho tam giác ABC vuông tại A có AC=4cm, AB+BC=8cm. Tính \(tg\dfrac{B}{2}\)
B1... Cho \(\Delta ABC\) nhọn AB=c , AC= b , CB=a
CMR : \(\dfrac{a}{\sin a}=\dfrac{b}{\sin b}=\dfrac{c}{\sin c}\)
B2... Không dùng bảng số và m.tính . Hãy tính
a) \(\sin^212^o+\sin^222^o+\sin^232^o+\sin^258^o+\sin^268^o+\sin^278^o\)
b)\(\cos^215^o+\cos^225^o+\cos^235^o+\cos^255^o+\cos^265^o+\cos^275^o-3\)
c) \(4\cos^2\alpha-6\sin^2\alpha,\) biết \(\sin\alpha=\dfrac{1}{5}\)
d) \(\sin\alpha.\cos\alpha\) biết \(\tan\alpha+\cot\alpha=3\)
Trong hình 44, hệ thức nào trong các hệ thức sau là đúng ?
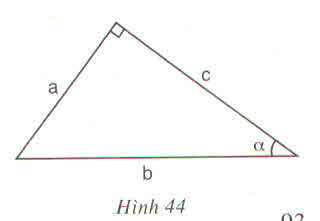
(A) \(\sin\alpha=\dfrac{b}{c}\) (B) \(cotg\alpha=\dfrac{b}{c}\) (C) \(tg\alpha=\dfrac{a}{c}\) (D) \(cotg\alpha=\dfrac{a}{c}\)
b) Trong hình 45, hệ thức nào trong các hệ thức sau không đúng ?
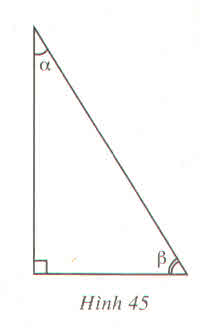
(A) \(\sin^2\alpha+\cos^2\alpha=1\)
(B) \(\sin\alpha=\cos\beta\)
(C) \(\cos\beta=\sin\left(90^0-\alpha\right)\)
(D) \(tg\alpha=\dfrac{\sin\alpha}{\cos\alpha}\)
1.
a. Cho Δ ABC vuông tại A có Cos B= o,6. tính tỉ số lượng giác góc C
b. Cho Tan α= 0,5. tính \(\dfrac{\sin\alpha+\cos\alpha}{\sin\alpha-\cos\alpha}\)
cho các góc α và β nhọn , α < β. Cmr:
a ) cos(β - α)=cosβcosα +sinβsinα
b) sin(β - α)=sinβcosα - sinβsinα
a) Biết sinα= \(\frac{1}{2}\). Tính cosα, tanα, cotα.
b) Biết cosα= \(\frac{2}{5}\). Tính sinα, tanα, cotα.
c) Biết tanα= 3. Tính cosα, sinα, cotα.
d) Biết cotα=\(\sqrt{3}\). Tính cosα, tanα, sinα.
e) Biết sinα= \(\frac{1}{\sqrt{3}}\). Tính cosα, tanα, cotα.
cho góc nhọn α. Biết cosα-sinα=\(\dfrac{1}{5}\)