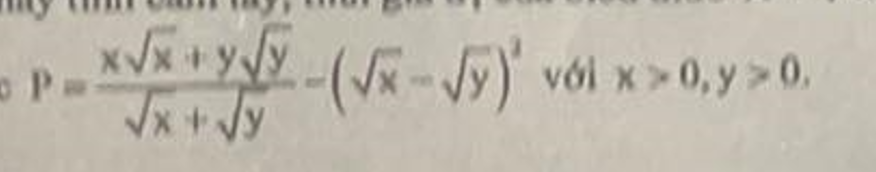P=\(x+y-\sqrt{xy}-x-y+2\sqrt{xy}\)=\(\sqrt{xy}\)
\(P=\dfrac{\left(\sqrt{x}\right)^3+\left(\sqrt{y}\right)^3}{\sqrt{x}+\sqrt{y}}-\left(\sqrt{x}-\sqrt{y}\right)^2\)
\(=\dfrac{\left(\sqrt{x}+\sqrt{y}\right)\left(x-\sqrt{xy}+y\right)}{\sqrt{x}+\sqrt{y}}-\left(x-2\sqrt{xy}+y\right)\)
\(=x-\sqrt{xy}+y-x+2\sqrt{xy}-y\)
\(=\sqrt{xy}\)