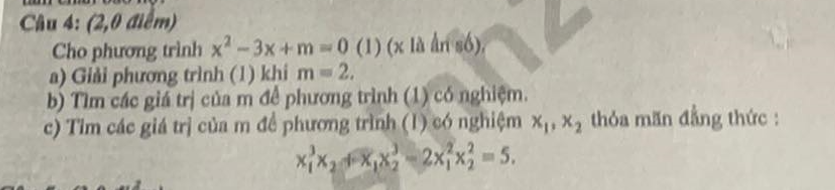a) thay m=2 vào pt (1) ta có
\(x^2-3x+2=0\)
<=>\(\left(x-1\right)\left(x+2\right)=0\)
<=>\(\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
b)để pt (1) có 1 nghiệm
<=>\(\Delta=0\)
<=>9-4m=0
<=>m=\(\dfrac{9}{4}\)
KL: vậy để pt (1) có 1 nghiệm thì m=\(\dfrac{9}{4}\)
c)để pt có 2 nghiệm pb thì \(\Delta>0\)
<=>9-4m>0
<=>m<\(\dfrac{9}{4}\)
áp dụng định lý Vi-ét ta có \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=m\end{matrix}\right.\)
theo đề bài ta có \(x_1^3x_2+x_1x_2^3-2x_1^2x_2^2=5\)
<=>\(x_1x_2\left(x_1+x_2\right)^2-4x^2_1x^2_{2^{ }}=5\)
<=>\(9m-4m^2=5\)
<=>\(4m^2-9m+5=0\)
<=>\(\left(m-1\right)\left(4m-5\right)=0\)
<=>\(\left[{}\begin{matrix}m=1\\m=\dfrac{5}{4}\end{matrix}\right.\)
KL: vậy với m =1 hoặc m=\(\dfrac{5}{4}\) thì pt có 2 nghiệm pb thỏa yêu cầu đề bài