Bài 1

a) Do AM là tia phân giác của \(\widehat{BAC}\) (gt)
\(\Rightarrow\widehat{BAM}=\widehat{CAM}\)
\(\Rightarrow\widehat{BAM}=\widehat{EAM}\)
Xét hai tam giác vuông: \(\Delta BAM\) và \(\Delta EAM\) có:
\(AM\) là cạnh chung
\(\widehat{BAM}=\widehat{EAM}\left(cmt\right)\)
\(\Rightarrow\Delta BAM=\Delta EAM\) (cạnh huyền - góc nhọn)
\(\Rightarrow MB=ME\) (hai cạnh tương ứng)
b) Xét hai tam giác vuông: \(\Delta BMD\) và \(\Delta EMC\) có:
\(MB=ME\left(cmt\right)\)
\(\widehat{BMD}=\widehat{EMC}\) (đối đỉnh)
\(\Rightarrow\Delta BMD=\Delta EMC\) (cạnh góc vuông - góc nhọn kề)
\(\Rightarrow BD=EC\) (hai cạnh tương ứng)
Bài 1:
a: Xét ΔABM vuông tại B và ΔAEM vuông tại E có
AM chung
\(\widehat{BAM}=\widehat{EAM}\)
Do đó: ΔABM=ΔAEM
=>MB=ME
b: Xét ΔMBD vuông tại B và ΔMEC vuông tại E có
MB=ME
\(\widehat{BMD}=\widehat{EMC}\)(hai góc đối đỉnh)
Do đó: ΔMBD=ΔMEC
=>BD=EC
Bài 2:
a: Xét ΔCAM vuông tại A và ΔCBM vuông tại B có
CM chung
CA=CB
Do đó: ΔCAM=ΔCBM
=>\(\widehat{ACM}=\widehat{BCM}\)
=>CM là phân giác của góc ACD
b: ΔCAM=ΔCBM
=>MA=MB
Xét ΔMAN vuông tại A và ΔMBD vuông tại B có
MA=MB
\(\widehat{AMN}=\widehat{BMD}\)(hai góc đối đỉnh)
Do đó: ΔMAN=ΔMBD
=>MN=MD
Bài 3:
a: Xét ΔADE và ΔACE có
AD=AC
\(\widehat{DAE}=\widehat{CAE}\)
AE chung
Do đó: ΔADE=ΔACE
=>\(\widehat{ADE}=\widehat{ACE}\)
=>\(\widehat{ACE}=90^0\)
=>EC\(\perp\)AB
b: Xét ΔEDK vuông tại D và ΔECB vuông tại C có
ED=EC
\(\widehat{DEK}=\widehat{CEB}\)(hai góc đối đỉnh)
Do đó: ΔEDK=ΔECB
=>DK=CB
c: Sửa đề: AK=AB
Ta có: AK=AD+DK
AB=AC+CB
mà AD=AC và DK=CB
nên AK=AB







 Giải giúp em câu cuối cùng cố gắng nhìn giúp ạ tại kêu bạn chụp giúp.Giải giúp mai em thi rồi
Giải giúp em câu cuối cùng cố gắng nhìn giúp ạ tại kêu bạn chụp giúp.Giải giúp mai em thi rồi







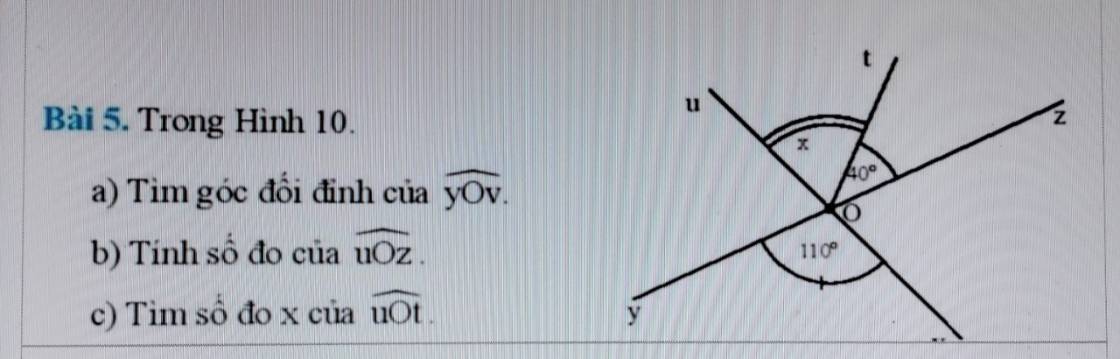 giúp em em cần gấp ạ mong mn giúp ạ
giúp em em cần gấp ạ mong mn giúp ạ