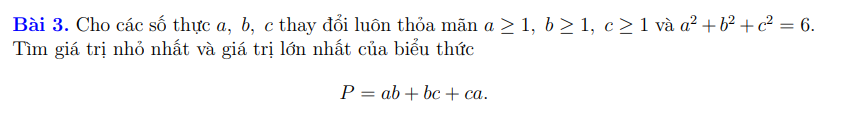a) \(5+\dfrac{x+4}{5}>x-\dfrac{x-2}{2}+\dfrac{x+3}{3}\)
\(\Leftrightarrow150+6\left(x+4\right)>150x-15\left(x-2\right)+10\left(x+3\right)\)
\(\Leftrightarrow150+6x+24>150x-15x+30+10x+30\)
\(\Leftrightarrow139x< 114\)
\(\Leftrightarrow x< \dfrac{114}{139}\)
b: \(x+1-\dfrac{x-1}{3}>\dfrac{2x+3}{2}+\dfrac{x}{3}+5\)
=>\(\dfrac{3\left(x+1\right)-x+1}{3}>\dfrac{3\left(2x+3\right)+2x+30}{6}\)
=>\(\dfrac{2\left(3x+3-x+1\right)}{6}>\dfrac{6x+9+2x+30}{6}\)
=>2(2x+4)>8x+39
=>4x+8>8x+39
=>-4x>31
=>\(x< -\dfrac{31}{4}\)
c: \(\dfrac{2x-3}{4}+\dfrac{3-x}{5}< =\dfrac{x+1}{3}+\dfrac{1}{2}\)
=>\(\dfrac{5\left(2x-3\right)+4\left(3-x\right)}{20}< =\dfrac{2x+2+3}{6}\)
=>\(\dfrac{10x-15+12-4x}{20}< =\dfrac{2x+5}{6}\)
=>\(\dfrac{6x-3}{20}< =\dfrac{2x+5}{6}\)
=>\(\dfrac{6\left(6x-3\right)}{120}< =\dfrac{20\left(2x+5\right)}{120}\)
=>36x-18<=40x+100
=>-4x<=118
=>\(x>=-\dfrac{59}{2}\)
d: \(x-\dfrac{x-1}{3}-\dfrac{2x-5}{5}+\dfrac{x+8}{6}>=15\)
=>\(\dfrac{30x-10\left(x-1\right)-6\left(2x-5\right)+5\left(x+8\right)}{30}>=15\)
=>\(30x-10x+10-12x+30+5x+40>=450\)
=>13x+80>=450
=>13x>=370
=>\(x>\dfrac{370}{13}\)
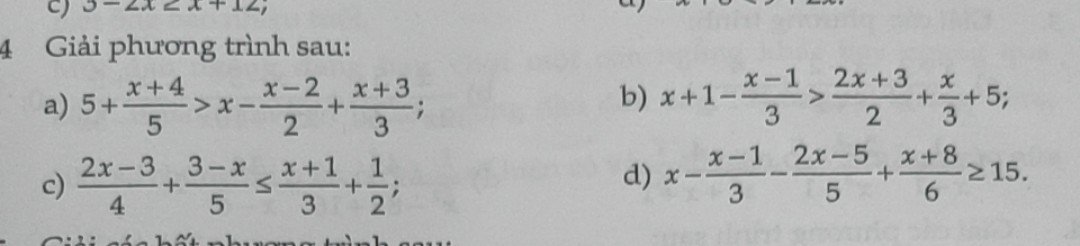
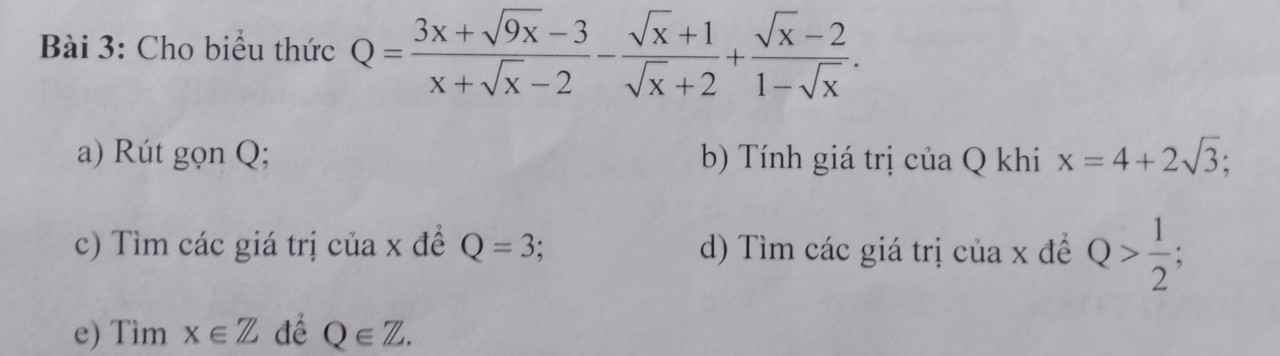giúp mình vs 