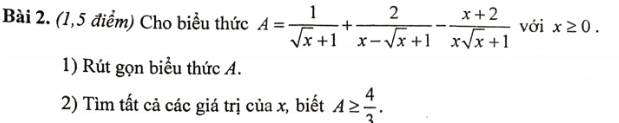1: \(A=\dfrac{1}{\sqrt{x}+1}+\dfrac{2}{x-\sqrt{x}+1}-\dfrac{x+2}{x\sqrt{x}+1}\)
\(=\dfrac{1}{\sqrt{x}+1}+\dfrac{2}{x-\sqrt{x}+1}-\dfrac{x+2}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\)
\(=\dfrac{x-\sqrt{x}+1+2\left(\sqrt{x}+1\right)-x-2}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\)
\(=\dfrac{-\sqrt{x}-1+2\sqrt{x}+2}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}=\dfrac{\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\)
\(=\dfrac{1}{x-\sqrt{x}+1}\)
2: A>=4/3
=>\(A-\dfrac{4}{3}>=0\)
=>\(\dfrac{1}{x-\sqrt{x}+1}-\dfrac{4}{3}>=0\)
=>\(\dfrac{3-4x+4\sqrt{x}-4}{3\left(x-\sqrt{x}+1\right)}>=0\)
=>\(-4x+4\sqrt{x}-1>=0\)
=>\(4x-4\sqrt{x}+1< =0\)
=>\(\left(2\sqrt{x}-1\right)^2< =0\)
mà \(\left(2\sqrt{x}-1\right)^2>=0\forall x>=0\)
nên \(2\sqrt{x}-1=0\)
=>\(\sqrt{x}=\dfrac{1}{2}\)
=>\(x=\dfrac{1}{4}\left(nhận\right)\)