Bài 3:
a: Xét ΔMNE vuông tại M và ΔDPE vuông tại P có
\(\widehat{MEN}=\widehat{DEP}\)
Do đó: ΔMNE\(\sim\)ΔDPE
b: Xét ΔEDP vuông tại D và ΔPDN vuông tại D có
\(\widehat{EPD}=\widehat{PND}\left(=\widehat{MNE}\right)\)
Do đó: ΔEDP\(\sim\)ΔPDN
Bài 2:
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=64\)
hay AC=8cm
Xét ΔABC có
H là trung điểm của AB
I là trung điểm của BC
Do đó: HI là đường trung bình của ΔBAC
Suy ra: HI//AC và \(HI=\dfrac{AC}{2}\)
hay \(HI=\dfrac{8}{2}=4\left(cm\right)\)
b: Xét tứ giác AHMC có
AC//MH
AC=MH
Do đó: AHMC là hình bình hành
mà \(\widehat{CAH}=90^0\)
nên AHMC là hình chữ nhật




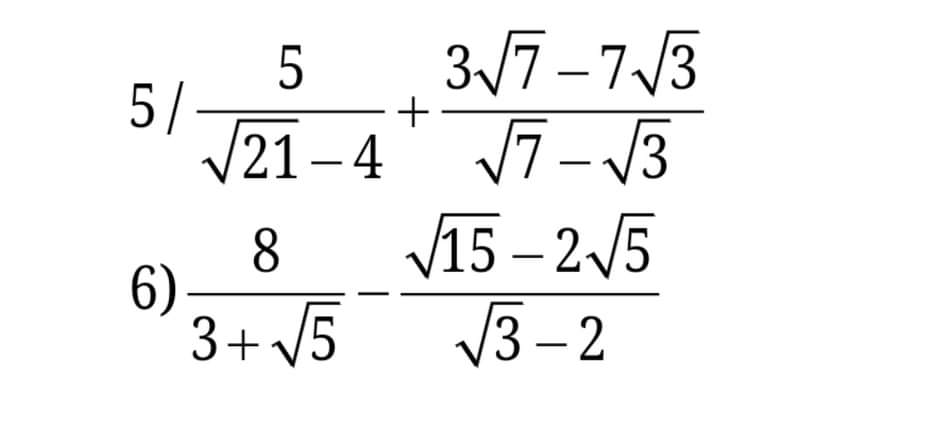 giúp mình với, cảm ơn
giúp mình với, cảm ơn