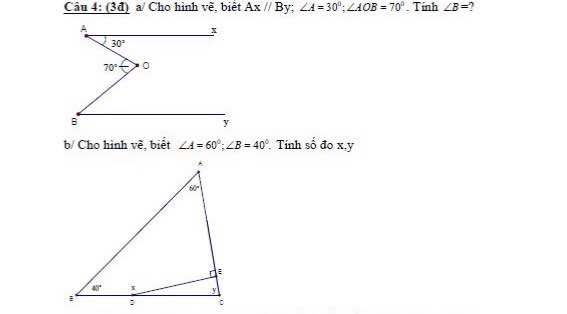
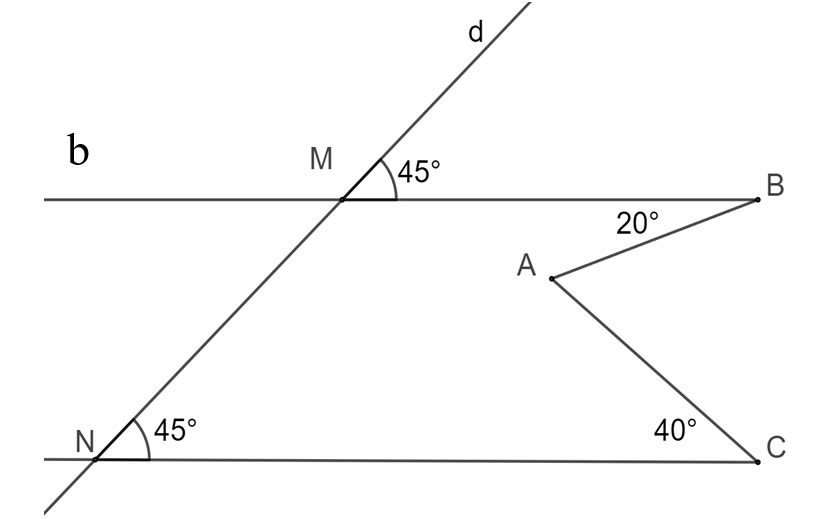
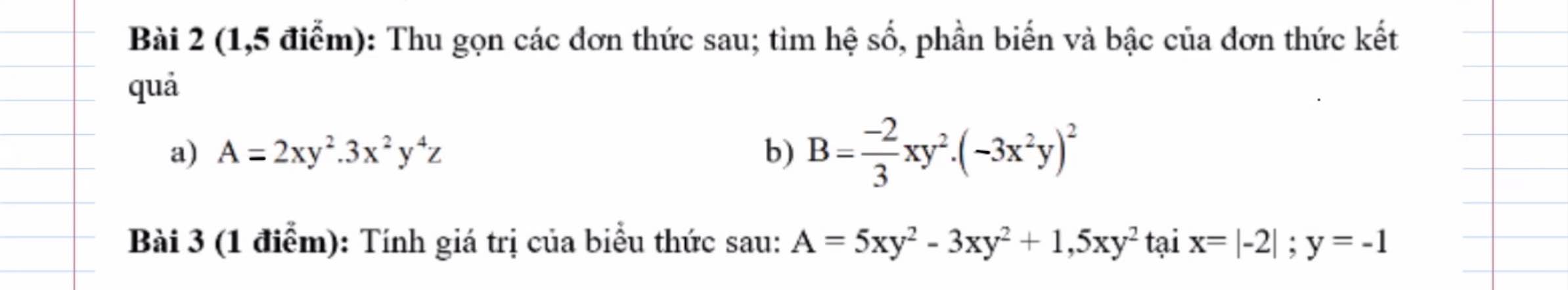i: ta có: \(\widehat{dMB}=\widehat{MNC}\left(=45^0\right)\)
mà hai góc này là hai góc ở vị trí đồng vị
nên BM//CN
ii: Ta có: \(\widehat{bMN}=\widehat{dMB}\)(hai góc đối đỉnh)
mà \(\widehat{dMB}=45^0\)
nên \(\widehat{bMN}=45^0\)
Qua A, kẻ tia AD nằm giữa hai tia AB và AC sao cho AD//BM//CN
AD//BM
=>\(\widehat{DAB}=\widehat{MBA}\)(hai góc so le trong)
=>\(\widehat{DAB}=20^0\)
Tacó: AD//NC
=>\(\widehat{DAC}=\widehat{ACN}\)(hai góc so le trong)
=>\(\widehat{DAC}=40^0\)
\(\widehat{BAC}=\widehat{BAD}+\widehat{CAD}=20^0+40^0=60^0\)
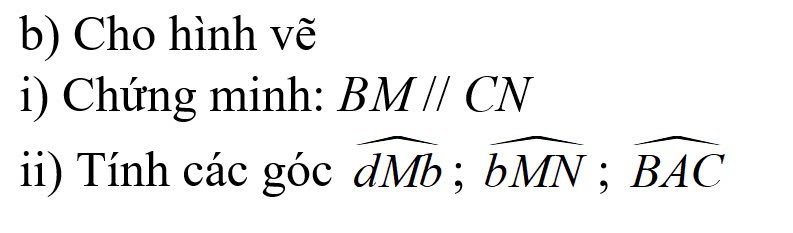 giúp mình vs
giúp mình vs