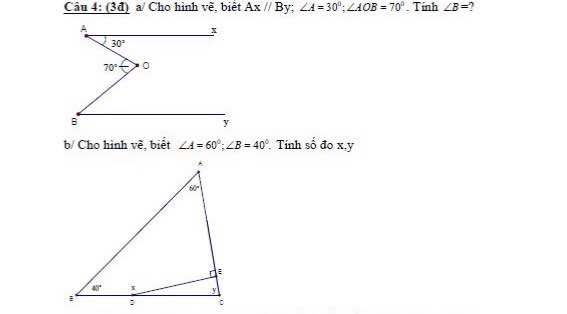
Câu 4a.
Kẻ tia $Om\parallel Ax$ như hình:
Vì $Ax\parallel Om$ nên $\widehat{AOm}=\widehat{xAO}=30^0$ (hai góc so le trong)
$\Rightarrow \widehat{mOB}=\widehat{AOB}-\widehat{AOm}=70^0-30^0=40^0$
$Ax\parallel By, Ax\parallel Om\Rightarrow By\parallel Om$
$\Rightarrow \widehat{B}=\widehat{mOB}=40^0$ (hai góc so le trong)
a) Trên nửa mặt phẳng bờ OB chứa điểm A, kẻ tia Oz//Ax//By
Ta có: Oz//Ax(cách vẽ)
\(\Rightarrow\widehat{xAO}=\widehat{AOz}=30^0\)( 2 góc so le trong)
Ta có: \(\widehat{AOz}+\widehat{zOB}=\widehat{AOB}\)
\(\Rightarrow\widehat{zOB}=\widehat{AOB}-\widehat{AOz}=70^0-30^0=40^0\)
Ta có: Oz//By
\(\Rightarrow\widehat{B}=\widehat{zOB}=40^0\)( 2 góc so le trong)
b) Xét tam giác ABC có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)( tổng 3 góc trong tam giác)
\(\Rightarrow\widehat{C}=180^0-\widehat{A}-\widehat{B}=180^0-60^0-40^0=80^0\)
\(\Rightarrow y=80^0\)
Xét tứ giác AEDB có:
\(\widehat{AED}+\widehat{EDB}+\widehat{ABD}+\widehat{BAE}=360^0\)
\(\Rightarrow\widehat{EDB}=360^0-\widehat{AED}-\widehat{ABD}-\widehat{BAE}=360^0-90^0-40^0-60^0=170^0\)
\(\Rightarrow x=170^0\)
Câu 4b.
Xét tứ giác $ABDE$ có:
$\widehat{A}+\widehat{B}+\widehat{D}+\widehat{E}=360^0$ (tổng 4 góc trong tứ giác)
$60^0+40^0+x+90^0=360^0$
$\Rightarrow x=170^0$
$\widehat{EDC}=180^0-x=180^0-170^0=10^0$
Xét tam giác $EDC$ vuông tại $E$:
$\widehat{E}+\widehat{EDC}+\widehat{C}=180^0$
$90^0+10^0+y=180^0$
$\Rightarrow y=80^0$




 giúp mình với, mình cảm ơn nhiều
giúp mình với, mình cảm ơn nhiều