a: Xét (O) có
MC là tiếp tuyến
MA là tiếp tuyến
Do đó: OM là tia phân giác của góc COA(1)
Xét (O) có
EC là tiếp tuyến
EB là tiếp tuyến
Do đó: OE là tia phân giác của góc COB(2)
Từ(1) và (2) suy ra \(\widehat{MOE}=\dfrac{1}{2}\left(\widehat{COA}+\widehat{COB}\right)=\dfrac{1}{2}\cdot180^0=90^0\)
b Xét ΔMOE vuông tại O có OC là đường cao
nên \(MO^2=MC\cdot ME\)
Đúng 0
Bình luận (0)






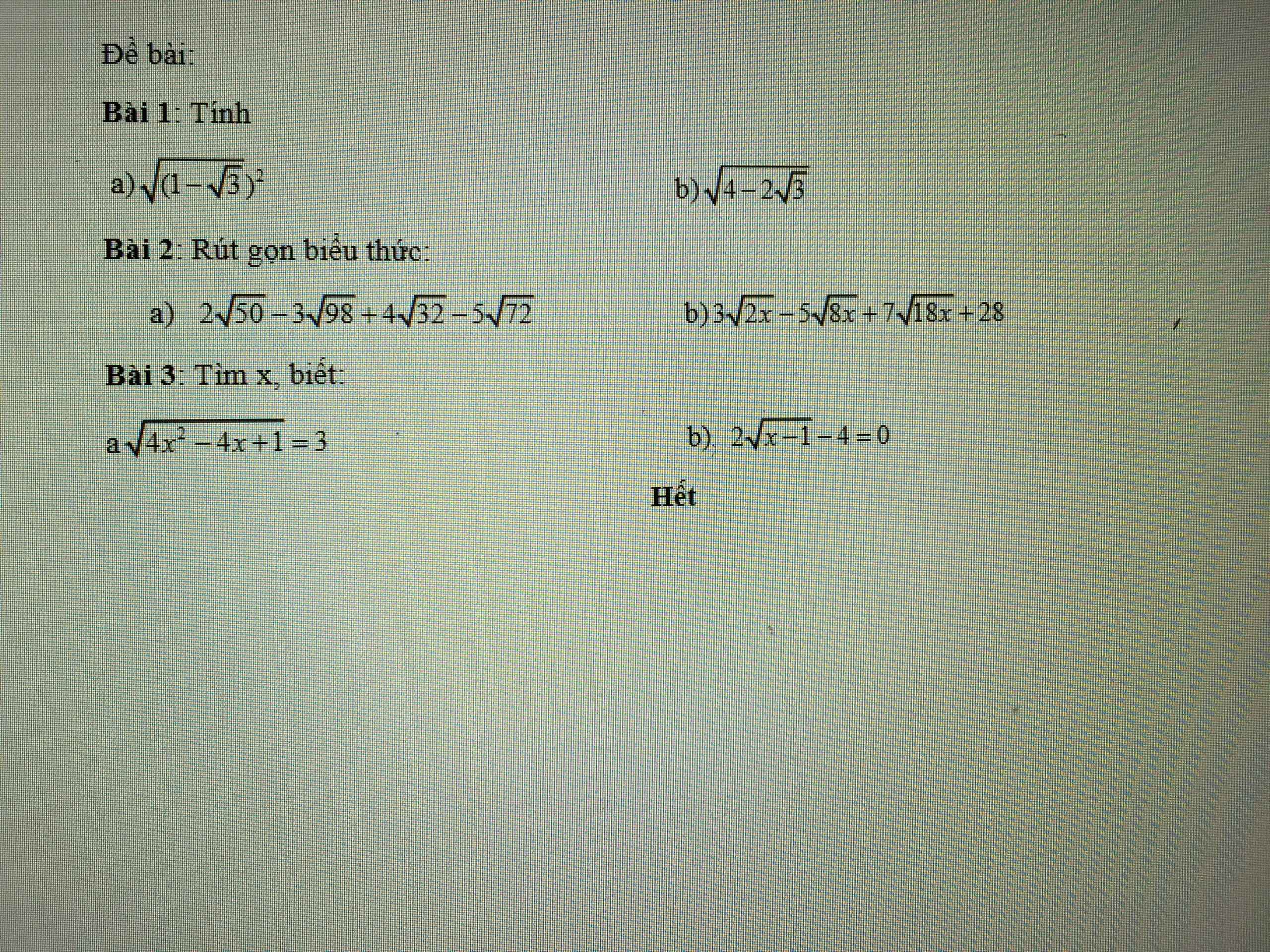 Giúp mình vs ạ. Cảm ơn trước ạ!
Giúp mình vs ạ. Cảm ơn trước ạ!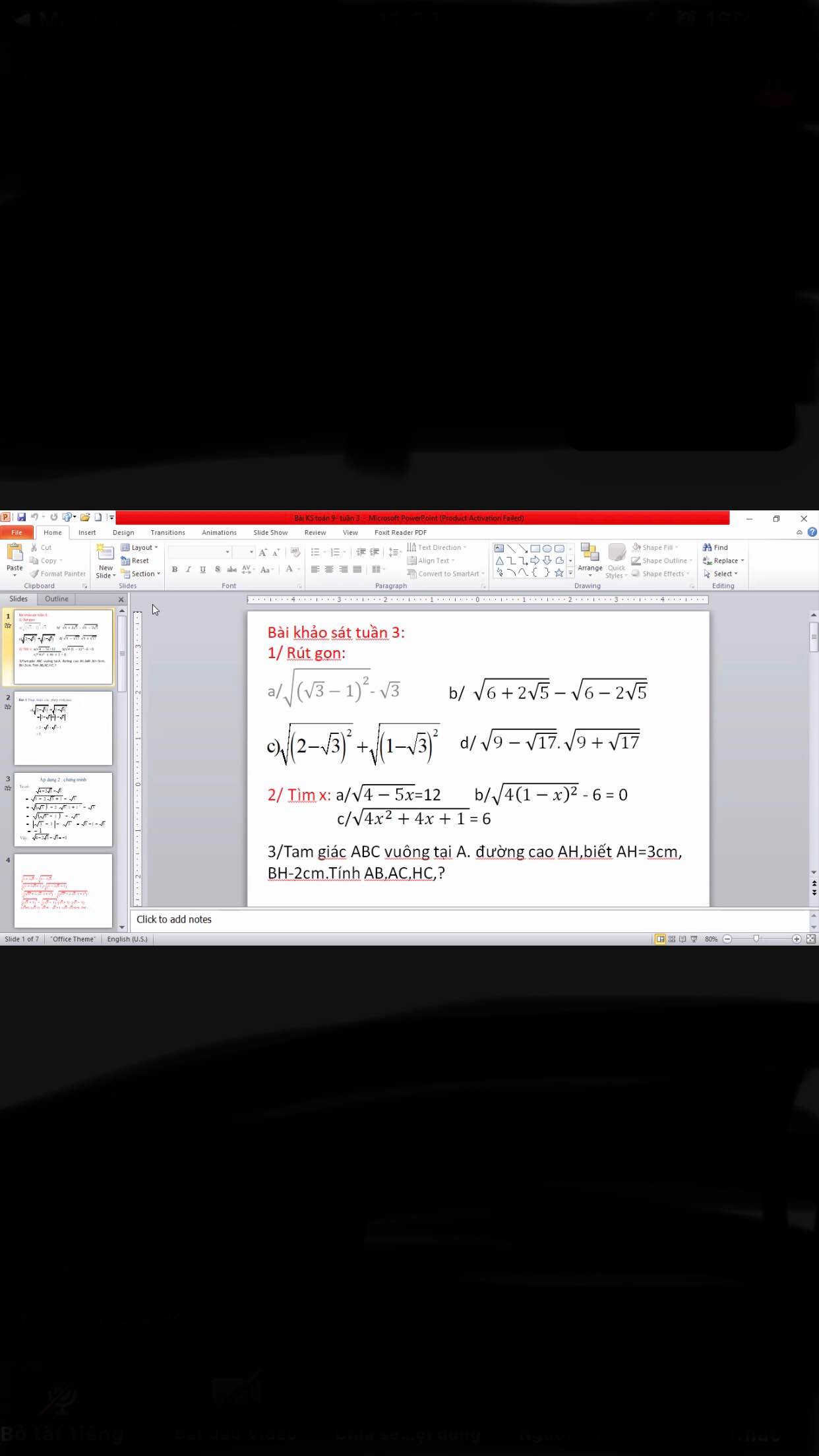

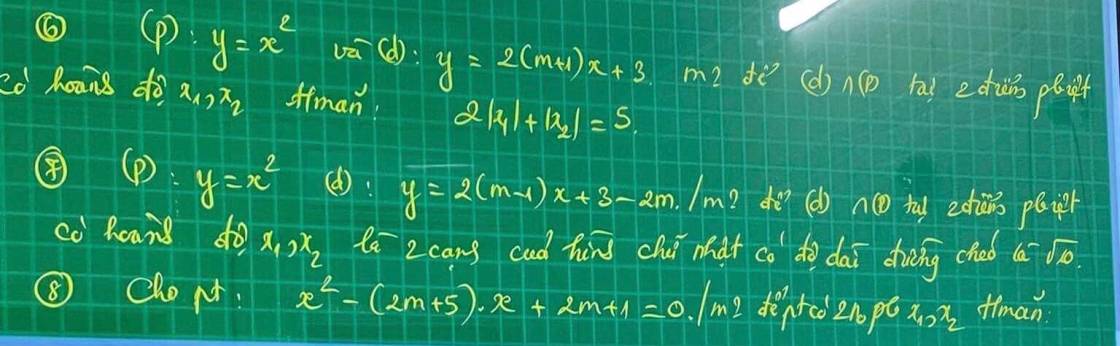
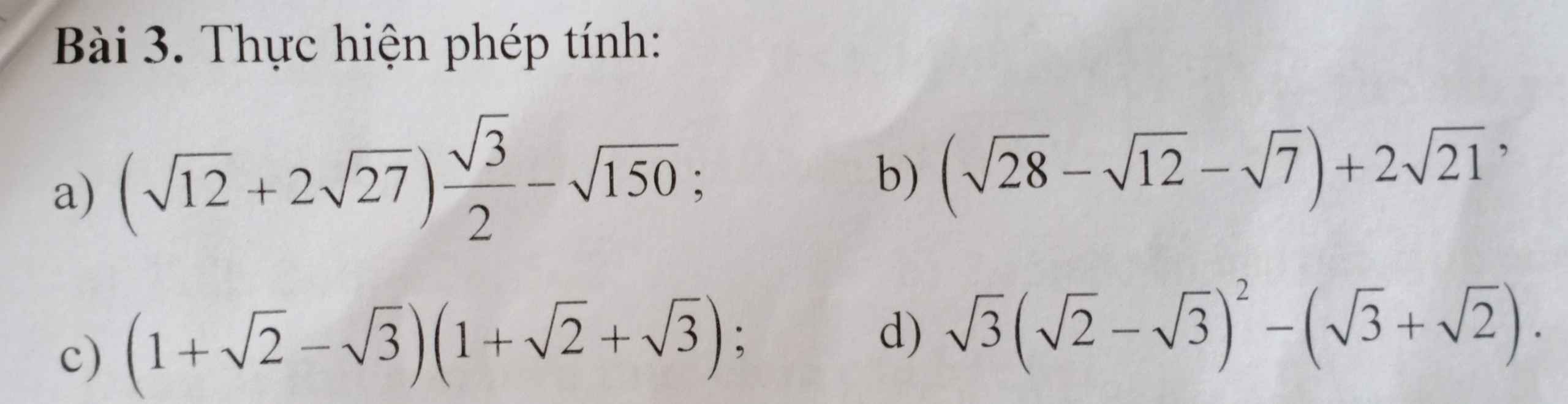 giúp mình vs ạ !
giúp mình vs ạ !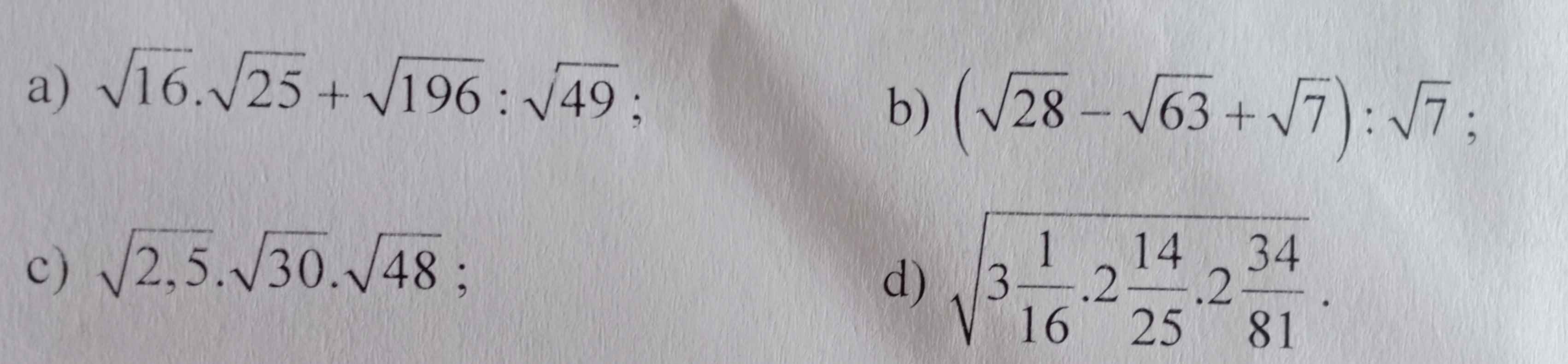 giúp mình vs ạ !
giúp mình vs ạ !