a) \(\left(\sqrt{12}+2\sqrt{27}\right)\dfrac{\sqrt{3}}{2}-\sqrt{150}=\left(2\sqrt{3}+6\sqrt{3}\right)\dfrac{\sqrt{3}}{2}-5\sqrt{6}\)
\(=3+9-5\sqrt{6}=12-5\sqrt{6}\)
b) \(\left(\sqrt{28}-\sqrt{12}-\sqrt{7}\right)+2\sqrt{21}=2\sqrt{7}-2\sqrt{3}-\sqrt{7}+2\sqrt{21}\)
\(=\sqrt{7}-2\sqrt{3}+2\sqrt{21}\)
c) \(\left(1+\sqrt{2}-\sqrt{3}\right)\left(1+\sqrt{2}+\sqrt{3}\right)=\left(1+\sqrt{2}\right)^2-3\)
\(=3+2\sqrt{2}-3=2\sqrt{2}\)
d) \(\sqrt{3}\left(\sqrt{2}-\sqrt{3}\right)^2-\left(\sqrt{3}+\sqrt{2}\right)=\sqrt{3}\left(5-2\sqrt{6}\right)-\left(\sqrt{3}+\sqrt{2}\right)\)
\(=5\sqrt{3}-6\sqrt{2}-\sqrt{3}-\sqrt{2}=4\sqrt{3}-7\sqrt{2}\)
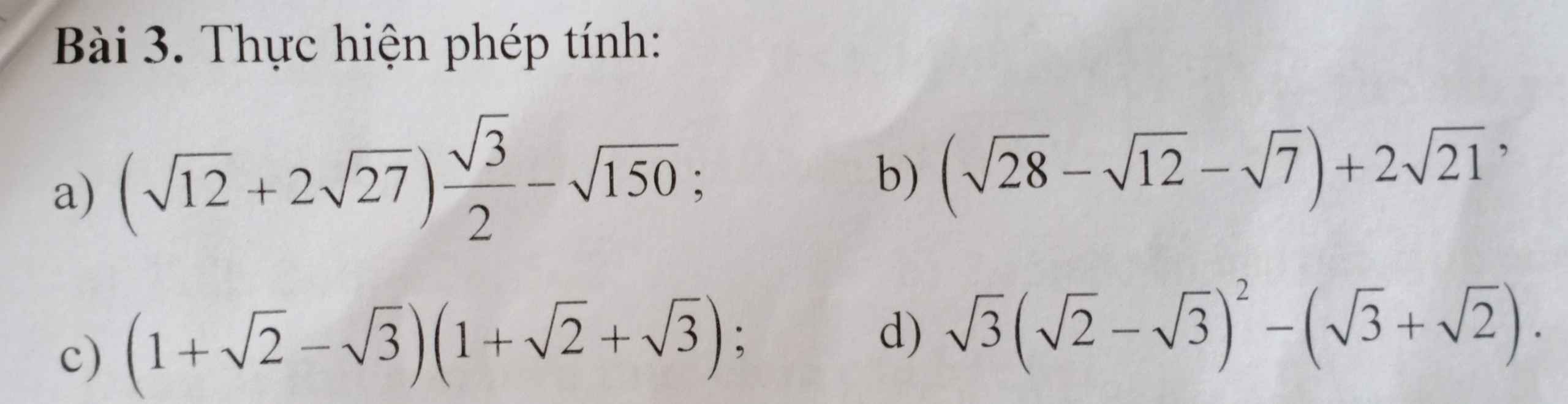 giúp mình vs ạ !
giúp mình vs ạ !




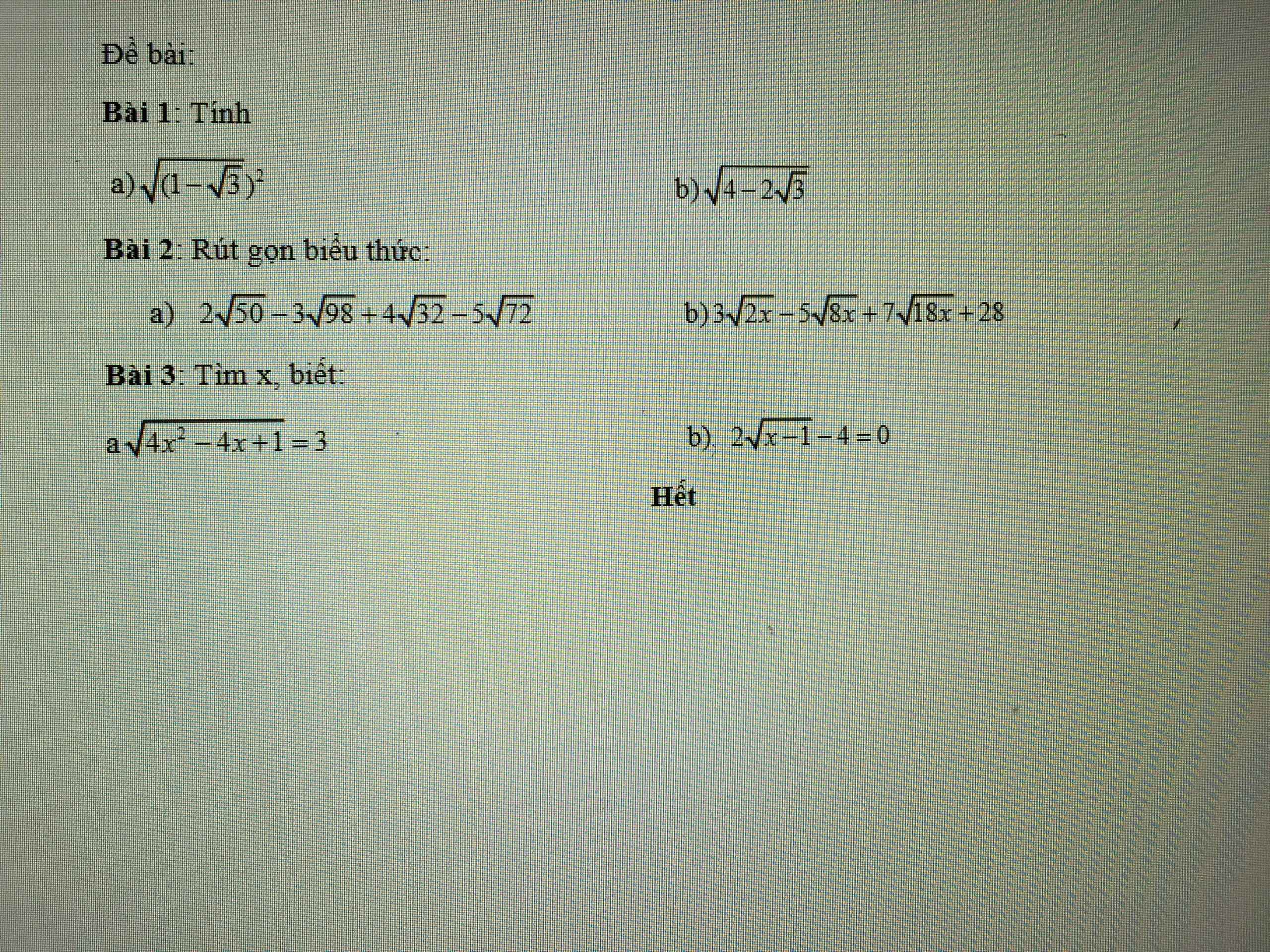 Giúp mình vs ạ. Cảm ơn trước ạ!
Giúp mình vs ạ. Cảm ơn trước ạ!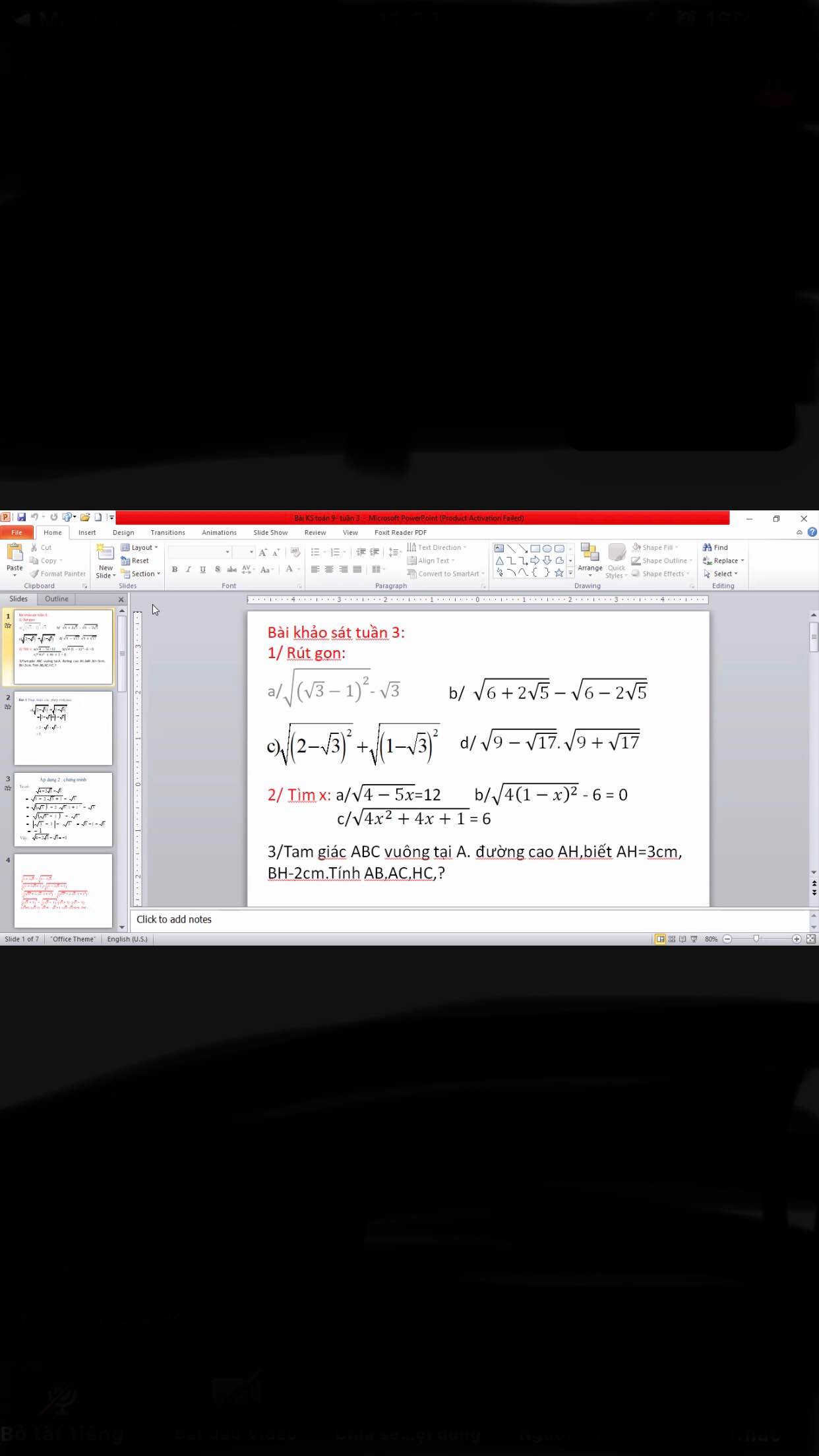

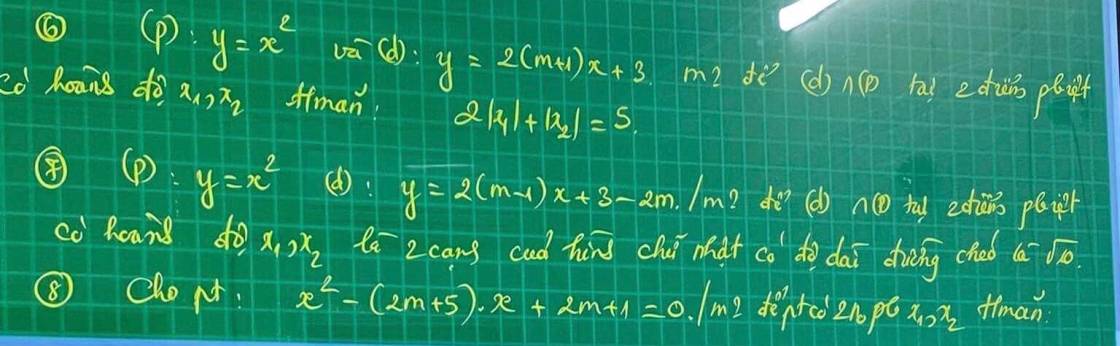
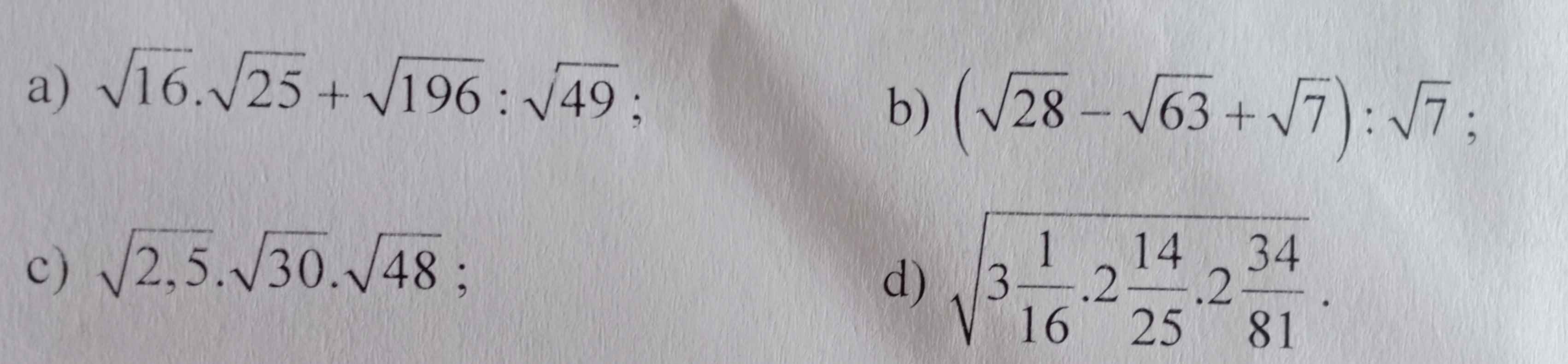 giúp mình vs ạ !
giúp mình vs ạ !