\(\dfrac{2x^2+1}{x^3+1}+\dfrac{1-x}{x^2-x+1}-\dfrac{1}{x+1}\left(x\ne-1\right)\)
\(=\dfrac{2x^2+1}{\left(x+1\right)\left(x^2-x+1\right)}+\dfrac{1-x}{x^2-x+1}-\dfrac{1}{x+1}\)
\(=\dfrac{2x^2+1}{\left(x+1\right)\left(x^2-x+1\right)}-\dfrac{\left(x-1\right)\left(x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}-\dfrac{x^2-x+1}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{2x^2+1-x^2+1-x^2+x-1}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{1}{x^2-x+1}\)
ĐKXĐ: x ≠ -1
(2x² + 1)/(x³ + 1) + (1 - x)/(x² - x + 1) - 1/(x + 1)
= [2x² + 1 + (1 - x)(x + 1) - (x² - x + 1)]/(x³ + 1)
= (2x² + 1 + 1 - x² - x² + x - 1)/(x³ + 1)
= (x + 1)/[(x + 1)(x² - x + 1)]
= 1/(x² - x + 1)
giúp mình bài này với ạ,ghi từng bước giúp mình lun ạ
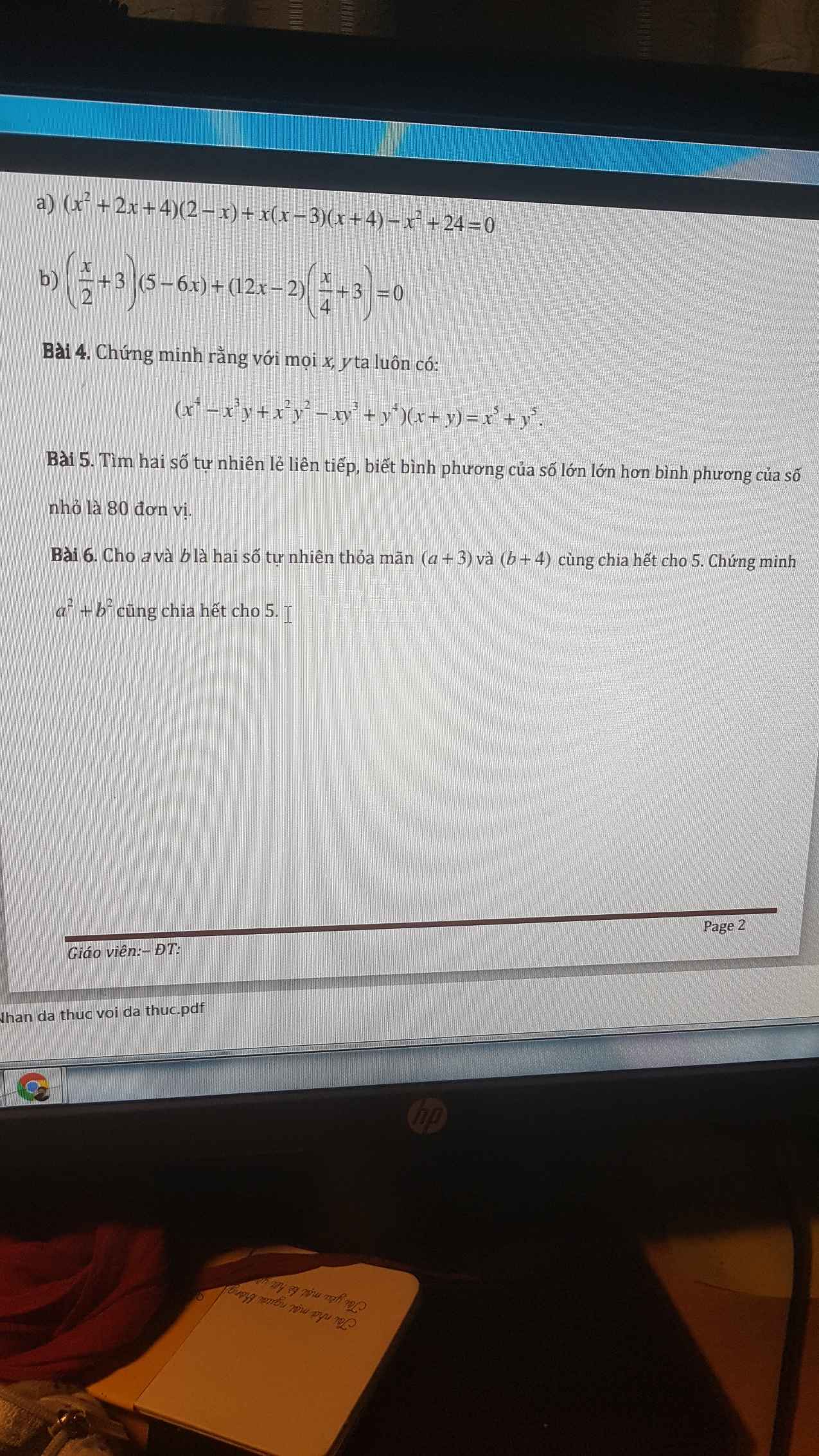
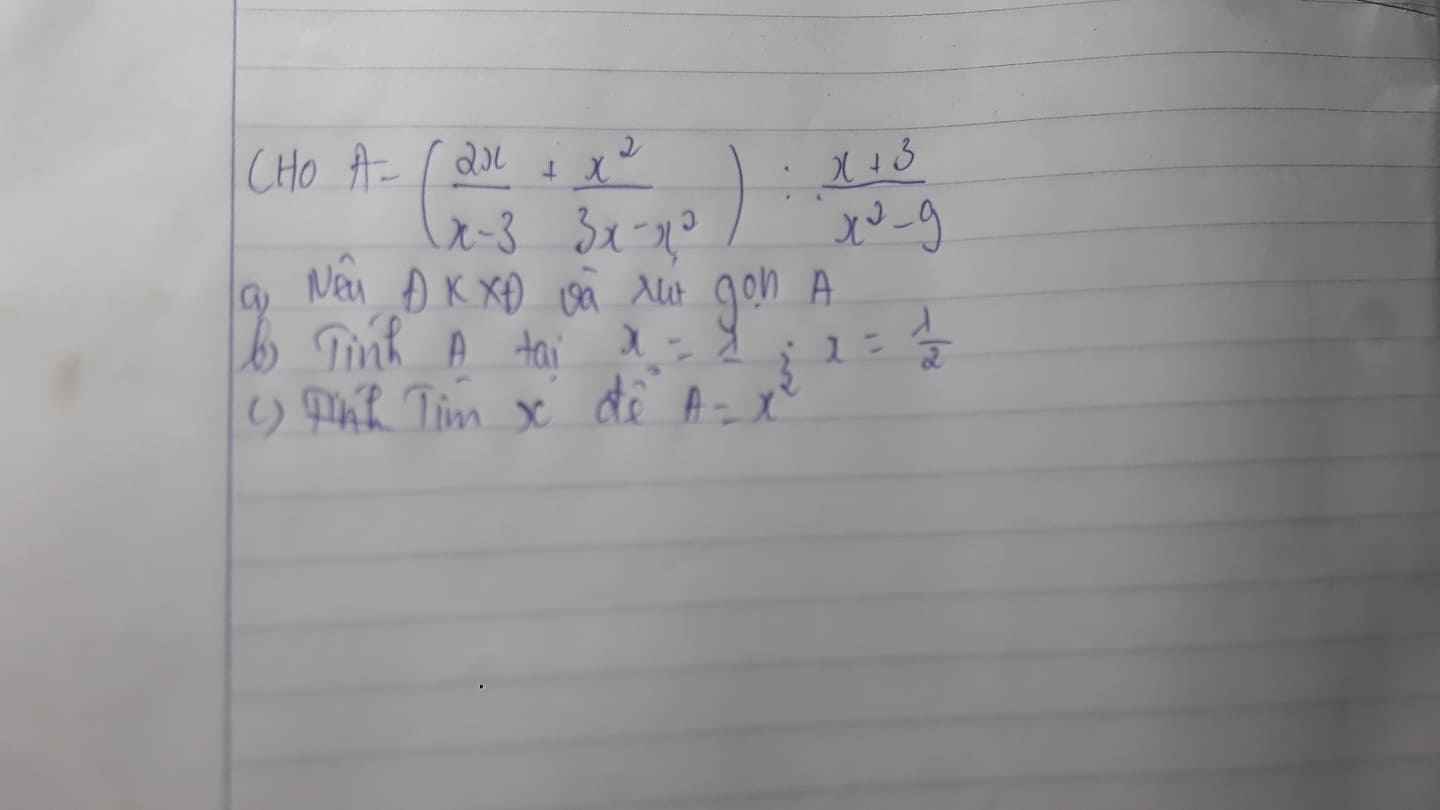
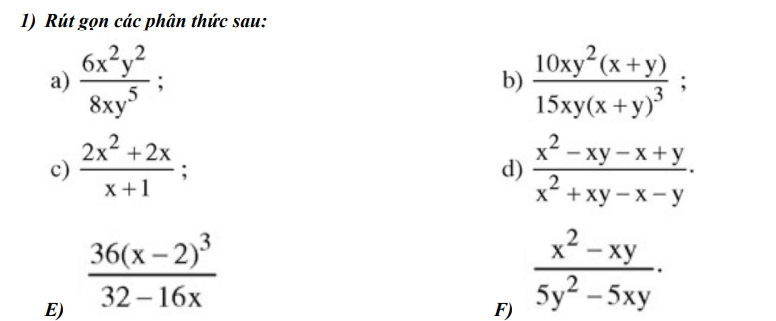
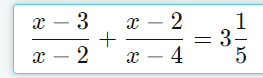mình cần gấp giúp mình với