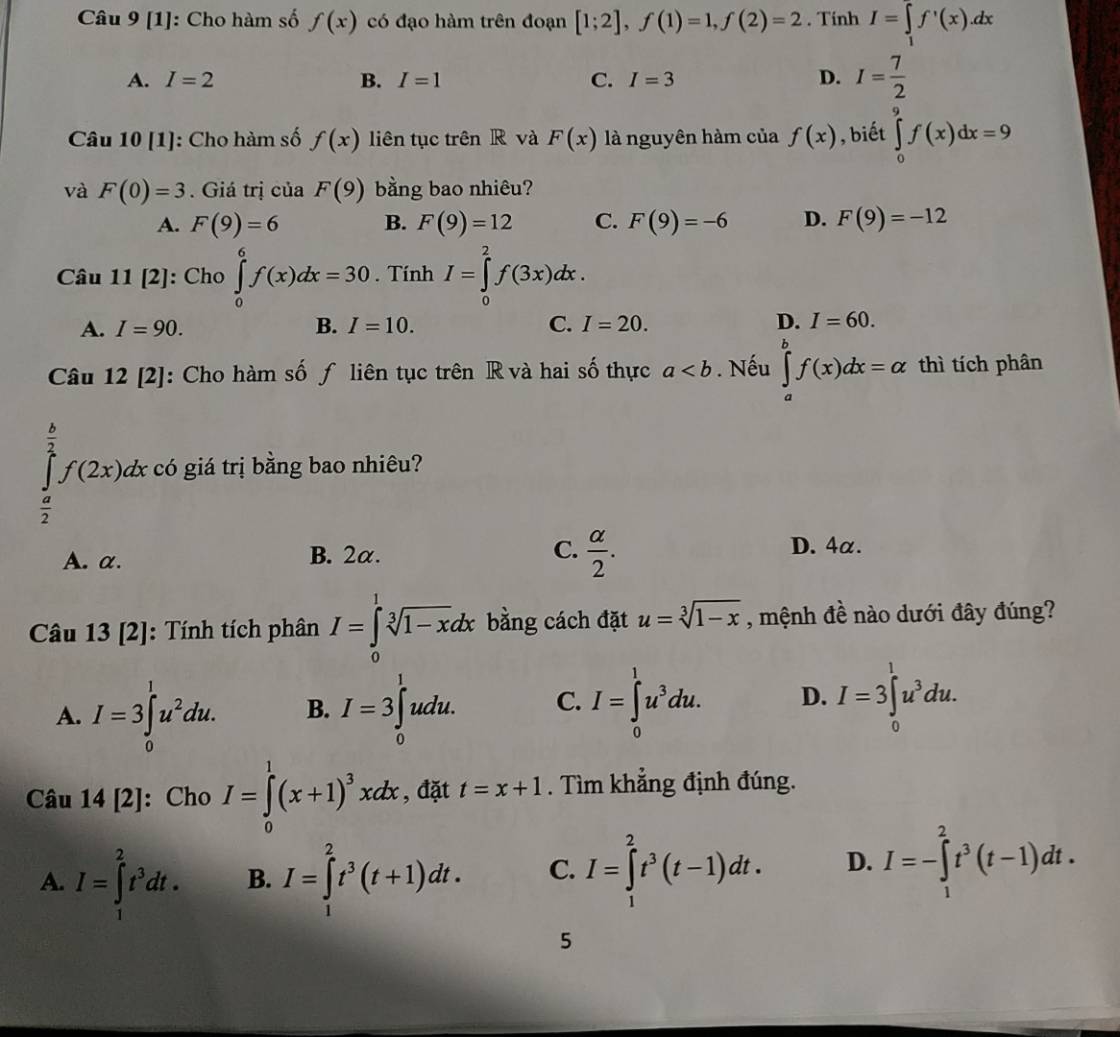9,
\(\int\limits^2_1f'\left(x\right)dx=f\left(x\right)|^2_1=f\left(2\right)-f\left(1\right)=2-1=1\)
10.
\(\int\limits^9_0f\left(x\right)dx=F\left(x\right)|^9_0=F\left(9\right)-F\left(0\right)\)
\(\Rightarrow F\left(9\right)-F\left(0\right)=9\Rightarrow F\left(9\right)=F\left(0\right)+9=12\)
11.
Đặt \(3x=u\Rightarrow3dx=du\Rightarrow dx=\dfrac{1}{3}du\)
\(\left\{{}\begin{matrix}x=0\Rightarrow u=0\\x=2\Rightarrow u=6\end{matrix}\right.\)
\(\Rightarrow\int\limits^2_0f\left(3x\right)dx=\int\limits^6_0f\left(u\right).\dfrac{1}{3}du=\dfrac{1}{3}\int\limits^6_0f\left(u\right)du=\dfrac{1}{3}\int\limits^6_0f\left(x\right)dx=\dfrac{1}{3}.30=10\)
12.
Đặt \(2x=u\Rightarrow2xdx=du\Rightarrow dx=\dfrac{1}{2}du\)
\(\left\{{}\begin{matrix}x=\dfrac{a}{2}\Rightarrow u=a\\x=\dfrac{b}{2}\Rightarrow u=b\end{matrix}\right.\)
\(\Rightarrow\int\limits^{\dfrac{b}{2}}_{\dfrac{a}{2}}f\left(2x\right)dx=\int\limits^b_af\left(u\right).\dfrac{1}{2}du=\dfrac{1}{2}\int\limits^b_af\left(u\right)du\)
\(=\dfrac{1}{2}\int\limits^b_af\left(x\right)dx=\dfrac{\alpha}{2}\)
13.
\(u=\sqrt[3]{1-x}\Rightarrow x=1-u^3\Rightarrow dx=-3u^2du\)
\(\left\{{}\begin{matrix}x=0\Rightarrow u=1\\x=1\Rightarrow u=0\end{matrix}\right.\)
\(\Rightarrow I=\int\limits^0_1u.\left(-3u^2\right)du=3\int\limits^1_0u^3du\)
14.
\(t=x+1\Rightarrow x=t-1\Rightarrow dx=dt\)
\(\left\{{}\begin{matrix}x=0\Rightarrow t=1\\x=1\Rightarrow t=2\end{matrix}\right.\)
\(\Rightarrow I=\int\limits^2_1t^3.\left(t-1\right)dt\)