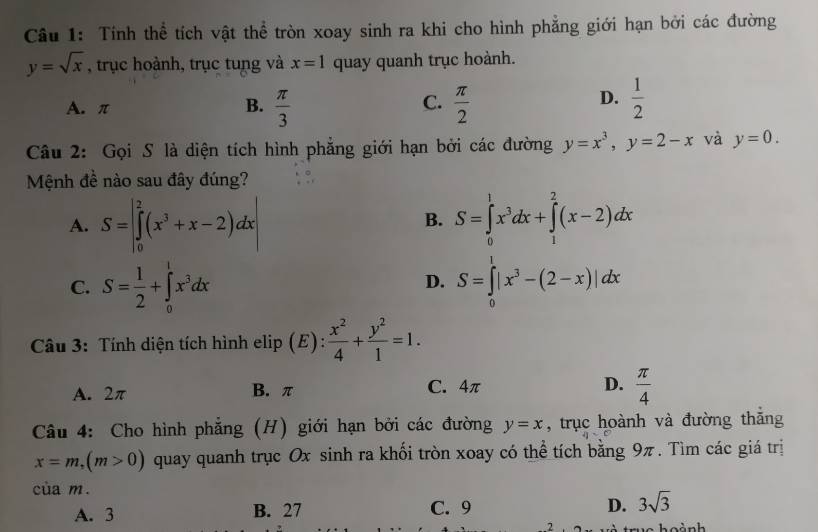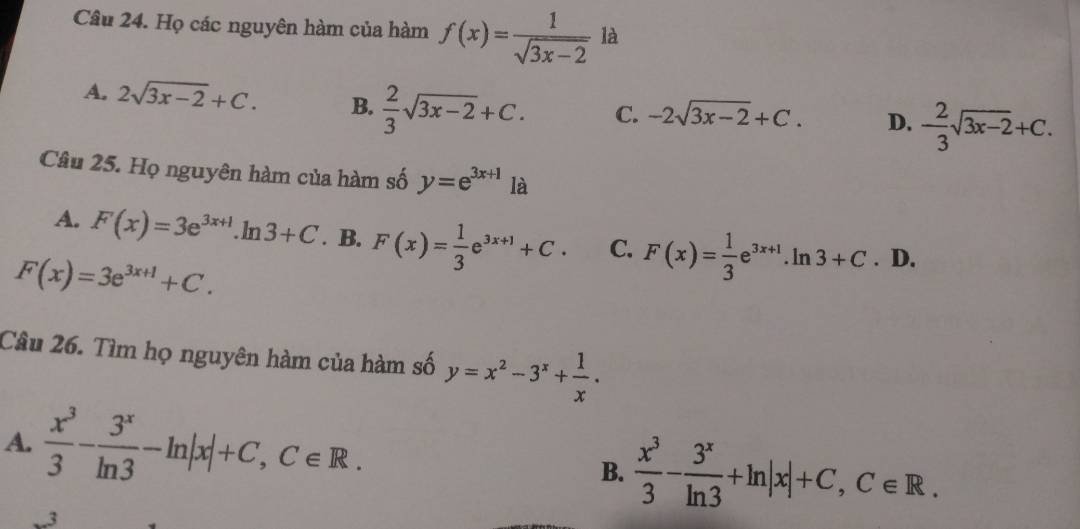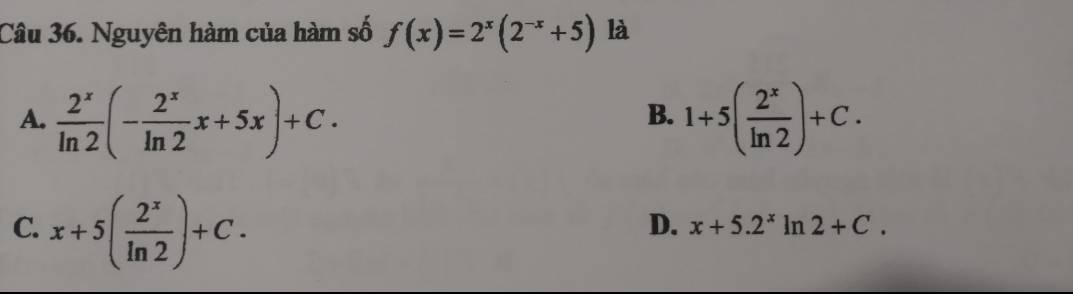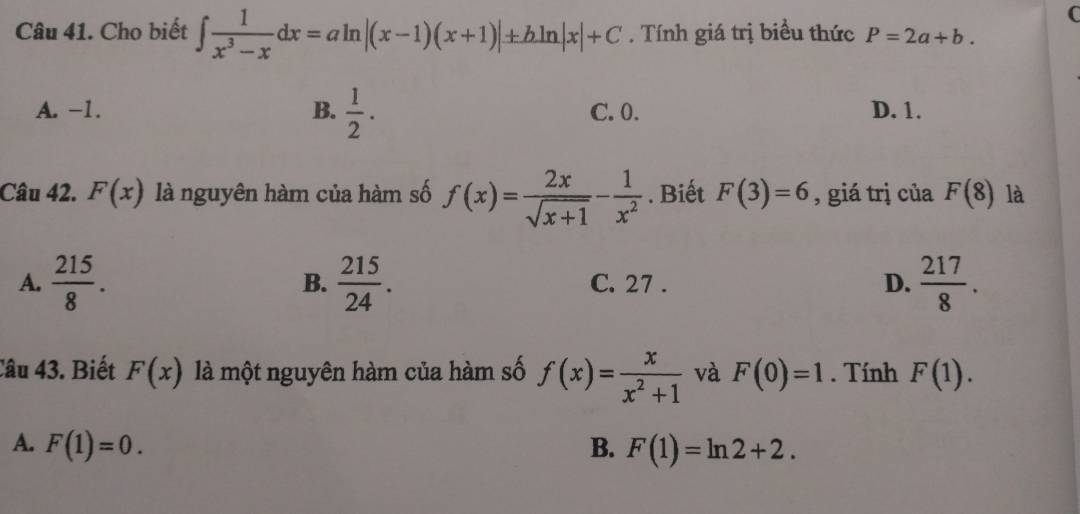1.
\(\sqrt{x}=0\Rightarrow x=0\)
\(\Rightarrow V=\pi\int\limits^1_0\left(\sqrt{x}\right)^2dx=\pi\)
2.
Phương trình hoành độ các giao điểm:
\(x^3=0\Rightarrow x=0\)
\(2-x=0\Rightarrow x=2\)
\(x^3=2-x\Rightarrow x=1\)
\(\Rightarrow S=\int\limits^1_0\left|x^3\right|dx+\int\limits^2_1\left|2-x\right|dx=\int\limits^1_0x^3dx+\int\limits^2_1\left(2-x\right)dx\)
\(=\dfrac{1}{2}+\int\limits^1_0x^3dx\)
3.
\(\dfrac{x^2}{4}+\dfrac{y^2}{1}=1\Rightarrow y^2=1-\dfrac{x^2}{4}\)
\(\Rightarrow y=\pm\sqrt{1-\dfrac{x^2}{4}}\)
Hoành độ giao điểm: \(\sqrt{1-\dfrac{x^2}{4}}=0\Rightarrow x=\pm2\)
\(\Rightarrow S=2\int\limits^2_{-2}\sqrt{1-\dfrac{x^2}{4}}dx\)
Đặt \(x=2sint\Rightarrow dx=2cost.dt\)
\(\left\{{}\begin{matrix}x=-2\Rightarrow t=-\dfrac{\pi}{2}\\x=2\Rightarrow t=\dfrac{\pi}{2}\end{matrix}\right.\)
\(\Rightarrow S=2\int\limits^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}\sqrt{1-cos^2t}.2cost.dt=2\int\limits^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}2cos^2tdt\)
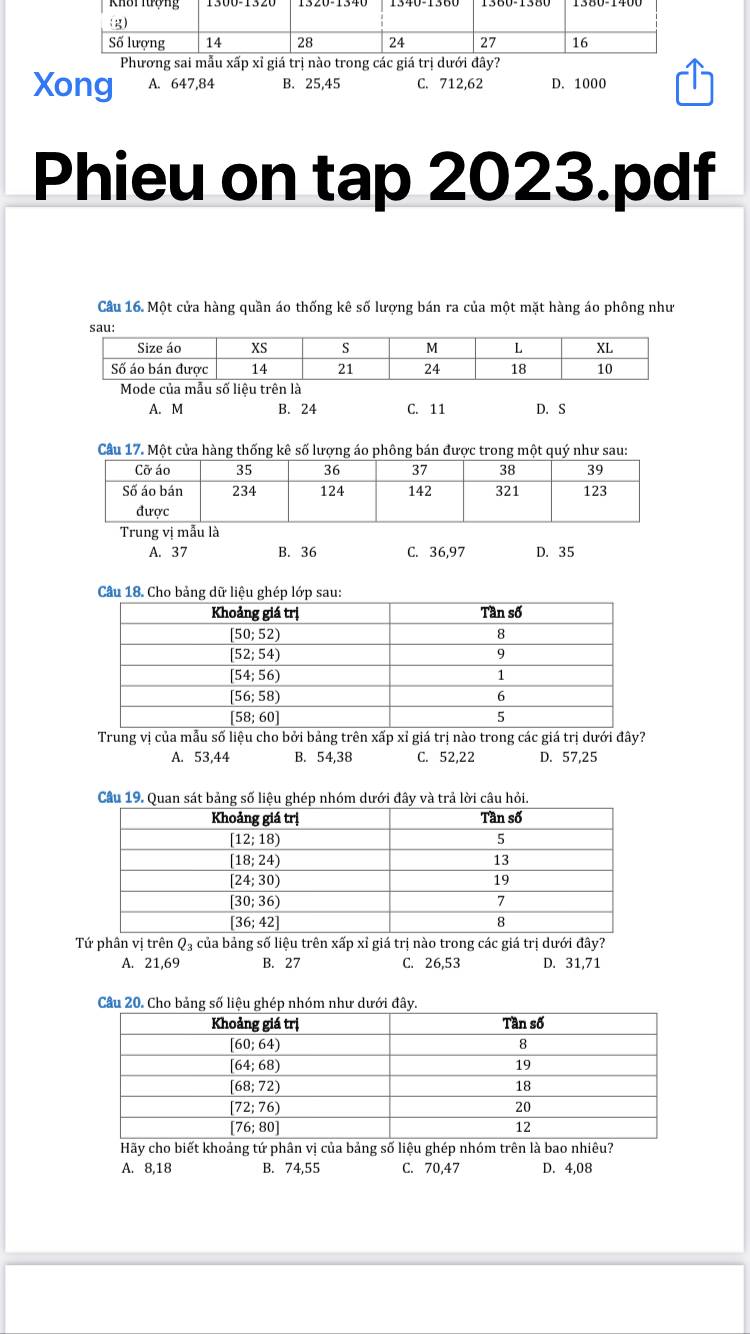
\(=2\int\limits^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}\left(cos2t+1\right)dt=\left(sin2t+2t\right)|^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}=2\pi\)
4.
\(V=\pi\int\limits^m_0x^2dx=\dfrac{\pi.x^3}{3}|^m_0=\dfrac{\pi}{3}.m^3=9\pi\)
\(\Rightarrow m^3=27\Rightarrow m=3\)
27.
\(y'\left(2\right)=-4\) ; \(y\left(2\right)=-3\)
Phương trình tiếp tuyến:
\(y=-4\left(x-2\right)-3=-4x+5\)
\(\Rightarrow S=\int\limits^2_0\left|-4x+5-\left(1-x^2\right)\right|dx=\int\limits^2_0\left(x^2-4x+4\right)dx=\dfrac{8}{3}\)
28.
Elip có các đỉnh (-3;0);(3;0);(0;-1);(0;1) nên độ dài 2 đường chéo lần lượt là 2 và 6
Diện tích hình thoi là: \(\dfrac{2.6}{2}=6\)
\(\dfrac{x^2}{9}+\dfrac{y^2}{1}=1\Rightarrow y=\pm\sqrt{1-\dfrac{x^2}{9}}\)
\(\Rightarrow S_{elip}=2\int\limits^3_{-3}\sqrt{1-\dfrac{x^2}{9}}dx\)
Đặt \(x=3sint\Rightarrow dx=3cost.dt\) ; \(\left\{{}\begin{matrix}x=-3\Rightarrow t=-\dfrac{\pi}{2}\\x=3\Rightarrow t=\dfrac{\pi}{2}\end{matrix}\right.\)
\(\Rightarrow S_{elip}=2\int\limits^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}cost.3costdt=\int\limits^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}6cos^2tdt\)
\(=\int\limits^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}\left(3cos2t+3\right)=\left(\dfrac{3}{2}sin2t+3t\right)|^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}=3\pi\)
\(\Rightarrow\dfrac{S_1}{S_2}=\dfrac{3\pi}{6}=\dfrac{\pi}{2}\)
29.
Hoành độ giao điểm: \(e^x=k\Rightarrow x=ln\left(k\right)\)
Thể tích khối tròn xoay:
\(V=\pi\int\limits^{ln\left(k\right)}_0k^2dx-\int\limits^{ln\left(k\right)}_0e^{2x}dx=\pi k^2.ln\left(k\right)-\dfrac{\pi}{2}.\left(k^2-1\right)\)
\(\Rightarrow\pi\left(k^2.ln\left(k\right)-\dfrac{k^2}{2}+\dfrac{1}{2}\right)=\pi\left(ln16-\dfrac{3}{2}\right)\)
\(\Rightarrow\left\{{}\begin{matrix}k^2.ln\left(k\right)=ln16\\-\dfrac{k^2}{2}+\dfrac{1}{2}=-\dfrac{3}{2}\end{matrix}\right.\)
\(\Rightarrow k=2\)