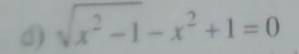\(đkx\ge1\\ \sqrt{x^2-1}-\left(x^2-1\right)=0\\ \sqrt{x^2-1}\left(1-\sqrt{x^2-1}\right)=0\\ \left[{}\begin{matrix}\sqrt{x^2-1}=0\\1-\sqrt{x^2-1}=0\end{matrix}\right.=>\left[{}\begin{matrix}x^2-1=0\\\sqrt{x^2-1}=-1\left(voli\right)\end{matrix}\right.=>x=1\left(thoaman\right);x=-1\left(kothoman\right)\)
`x^2 - 1 - sqrt(x^2-1) = 0`
Đặt `t = sqrt(x^2-1)`.
`-> t^2 - t = 0`
`-> t(t-1) = 0`
`-> sqrt(x^2-1) = 0` hoặc `sqrt(x^2-1) = 1`.
`-> x = +-1` hoặc `x = +-sqrt2`.
d: \(\Leftrightarrow\sqrt{x^2-1}=x^2-1\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)\left(x+1\right)>=0\\x^2-1=\left(x^2-1\right)^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x>=1\\x< =-1\end{matrix}\right.\\\left(x^2-1\right)\left(x^2-2\right)=0\end{matrix}\right.\)
\(\Leftrightarrow x\in\left\{1;-1;\sqrt{2};-\sqrt{2}\right\}\)