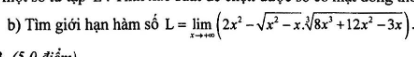c. Do mẫu số có nghiệm kép \(x=1\Rightarrow\)để giới hạn đã cho hữu hạn
\(\Rightarrow2\sqrt{1+ax^2}-bx-1=0\) có nghiệm kép \(x=1\)
Xét pt:
\(\sqrt{4+4ax^2}-bx-1=0\Leftrightarrow\sqrt{4+4ax^2}=bx+1\)
\(\Rightarrow4+4ax^2=\left(bx+1\right)^2=b^2x^2+2bx+1\)
\(\Rightarrow\left(4a-b^2\right)x^2-2bx+3=0\) (1)
Để (1) có nghiệm kép \(x=1\Rightarrow\left\{{}\begin{matrix}\Delta'=b^2-3\left(4a-b^2\right)=0\\\dfrac{b}{4a-b^2}=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}4a-b^2=\dfrac{b^2}{3}\\4a-b^2=b\end{matrix}\right.\) \(\Rightarrow b=\dfrac{b^2}{3}\Rightarrow\left[{}\begin{matrix}b=0\left(ktm\right)\\b=3\end{matrix}\right.\) \(\Rightarrow a=3\)
\(c=\lim\limits_{x\rightarrow1}\dfrac{2\sqrt{1+3x^2}-3x-1}{x\left(x-1\right)^2}=\dfrac{3}{8}\)
d.
\(\lim\limits_{x\rightarrow+\infty}\left(\dfrac{x^2+1+\left(x-2\right)\left(ax-b\right)}{x-2}\right)=\lim\limits_{x\rightarrow+\infty}\left(\dfrac{\left(a+1\right)x^2-\left(2a+b\right)x+2b+1}{x-2}\right)\)
Giới hạn đã cho hữu hạn khi và chỉ khi \(a+1=0\Rightarrow a=-1\)
Khi đó:
\(\lim\limits_{x\rightarrow+\infty}\left(\dfrac{\left(2-b\right)x+2b+1}{x-2}\right)=\lim\limits_{x\rightarrow+\infty}\left(\dfrac{2-b+\dfrac{2b+1}{x}}{1-\dfrac{2}{x}}\right)=2-b\)
\(\Rightarrow2-b=-5\Rightarrow b=7\)
\(\Rightarrow a+b=6\)



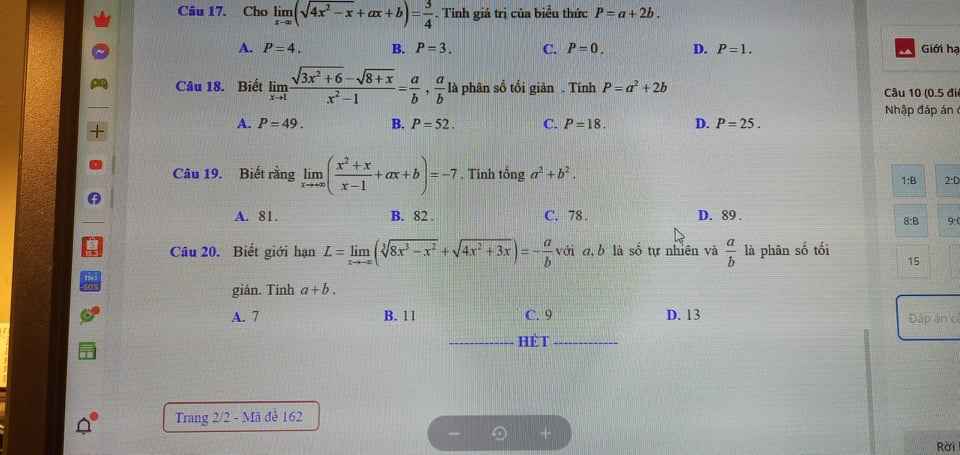
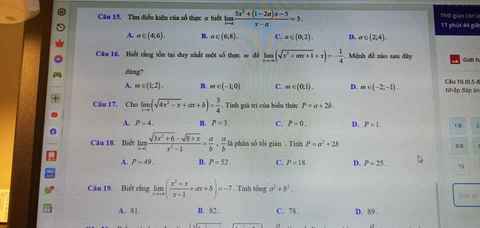
 với ạ cần gấp ngày mai
với ạ cần gấp ngày mai 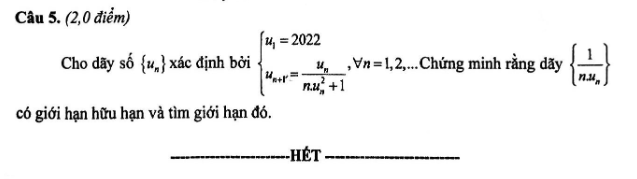 giúp em với em cảm ơn nhiều ạ
giúp em với em cảm ơn nhiều ạ