a) \(\dfrac{1}{\sqrt{x}-1}+\dfrac{1}{1+\sqrt{x}}+1=\dfrac{1}{\sqrt{x}-1}+\dfrac{1}{\sqrt{x}+1}+1=\dfrac{\left(\sqrt{x}+1\right)+\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}+1=\) \(\dfrac{2\sqrt{x}}{x-1}+1\)
b) \(\dfrac{1}{\sqrt{x}-2}-\dfrac{2}{\sqrt{x}+2}-\dfrac{\sqrt{x}}{4-x}=\dfrac{1}{\sqrt{x}-2}-\dfrac{2}{\sqrt{x}+2}+\dfrac{\sqrt{x}}{x-4}=\dfrac{\left(\sqrt{x}+2\right)-2\left(\sqrt{x}-2\right)+\sqrt{x}}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\) =
\(\dfrac{\sqrt{x}+2-2\sqrt{x}+4+\sqrt{x}}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\dfrac{6}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
c) Chưa biết làm





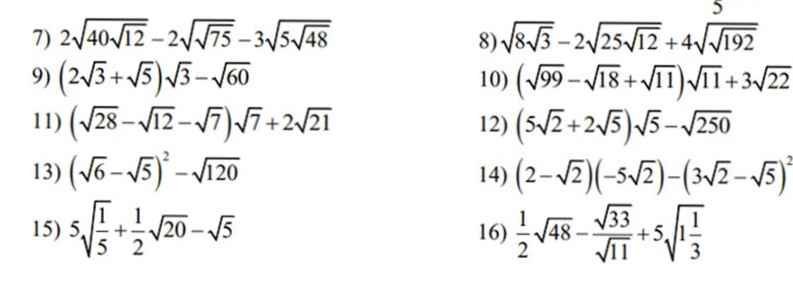

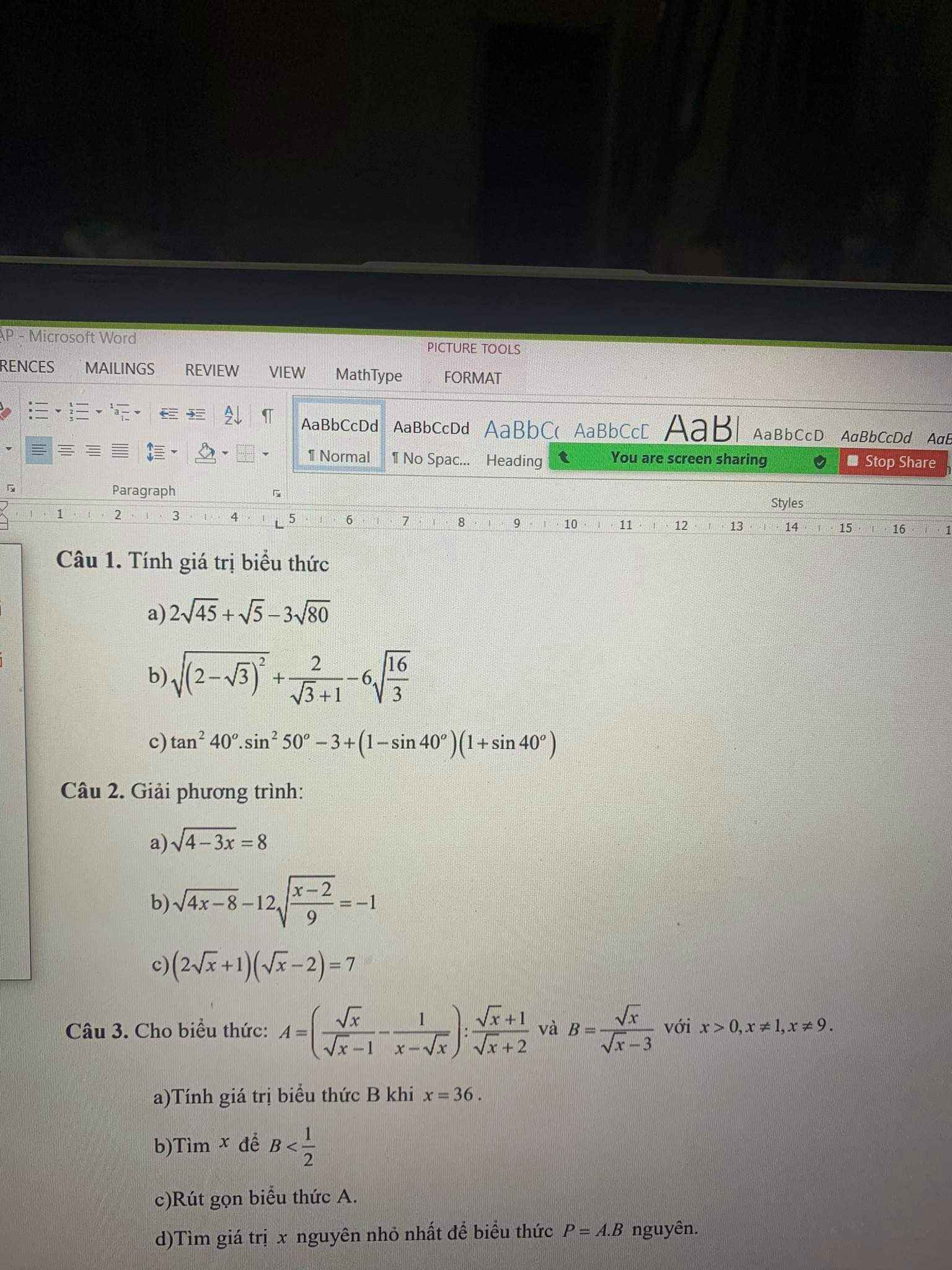

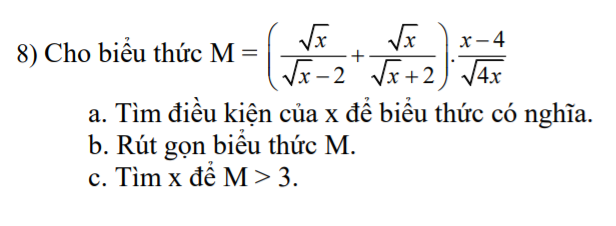
 Mn giúp mình bài 3 với ạ. Mình đang cần gấp lắm. Mình cảm ơn nhiều !
Mn giúp mình bài 3 với ạ. Mình đang cần gấp lắm. Mình cảm ơn nhiều !