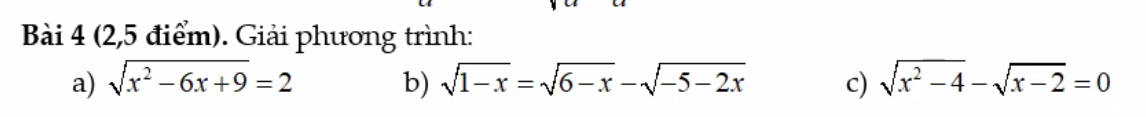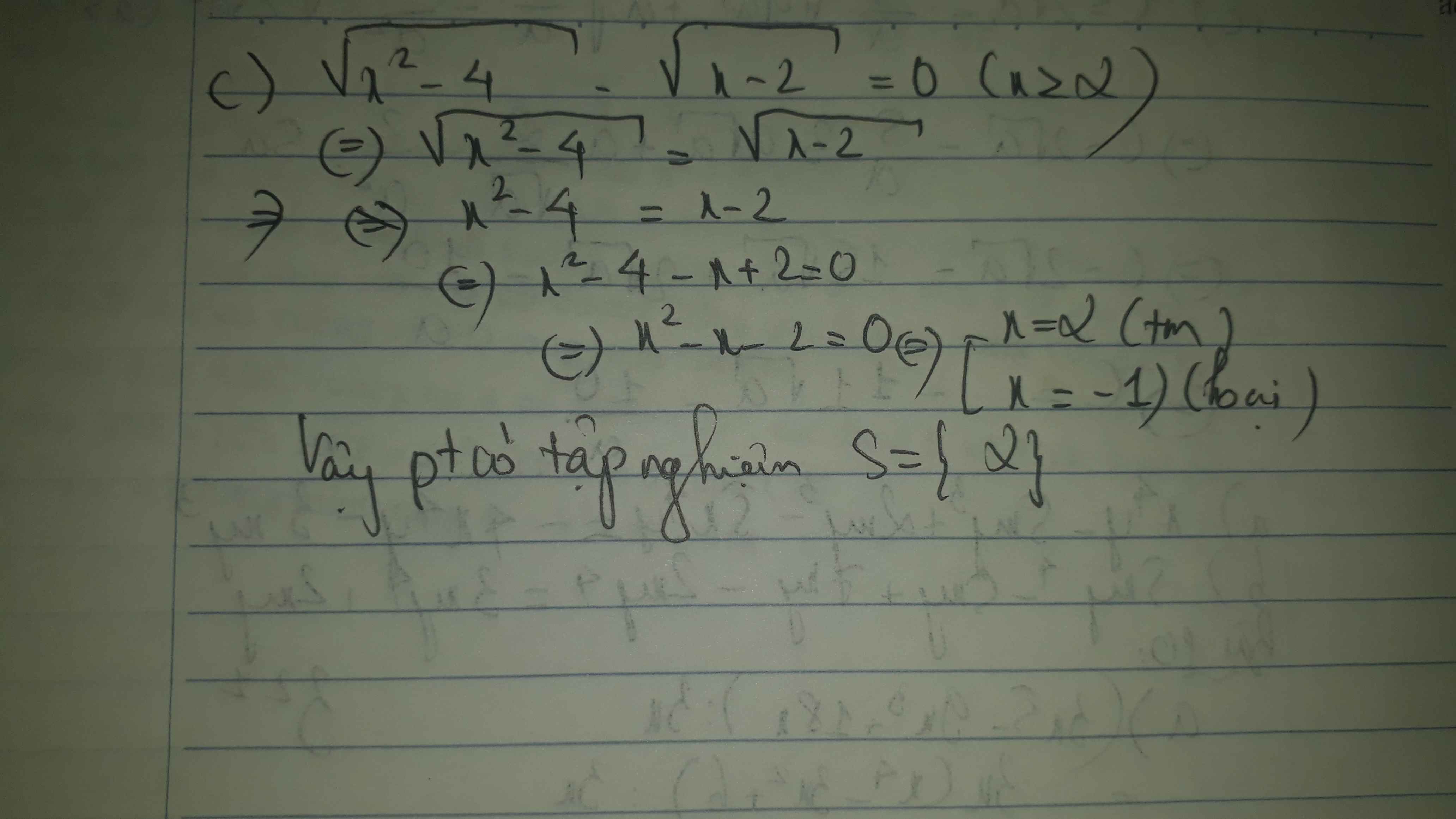a, \(\sqrt{x^2-6x+9}=2\)
\(\Leftrightarrow\sqrt{\left(x-3\right)^2}=2\)
\(\Leftrightarrow\left|x-3\right|=2\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=2\\x-3=-2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=1\end{matrix}\right.\)
a: Ta có: \(\sqrt{x^2-6x+9}=2\)
\(\Leftrightarrow\left(x-5\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=1\end{matrix}\right.\)
b, ĐK: \(x\le-\dfrac{5}{2}\)
\(\sqrt{1-x}=\sqrt{6-x}-\sqrt{-5-2x}\)
\(\Leftrightarrow\sqrt{1-x}+\sqrt{-5-2x}=\sqrt{6-x}\)
\(\Leftrightarrow1-x-5-2x+2\sqrt{\left(x-1\right)\left(2x+5\right)}=6-x\)
\(\Leftrightarrow\sqrt{2x^2+3x-5}=x+5\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x^2+3x-5=x^2+10x+25\\x+5\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2-7x-30=0\\x\ge-5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3\left(tm\right)\\x=10\left(l\right)\end{matrix}\right.\)
Vậy phương trình đã cho có nghiệm \(x=-3\).
c, ĐK: \(x\ge2\)
\(\sqrt{x^2-4}-\sqrt{x-2}=0\)
\(\Leftrightarrow\sqrt{\left(x+2\right)\left(x-2\right)}-\sqrt{x-2}=0\)
\(\Leftrightarrow\sqrt{x-2}\left(\sqrt{x+2}-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-2}=0\\\sqrt{x+2}=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=-1\left(l\right)\end{matrix}\right.\)
Vậy phương trình đã cho có nghiệm \(x=2\).