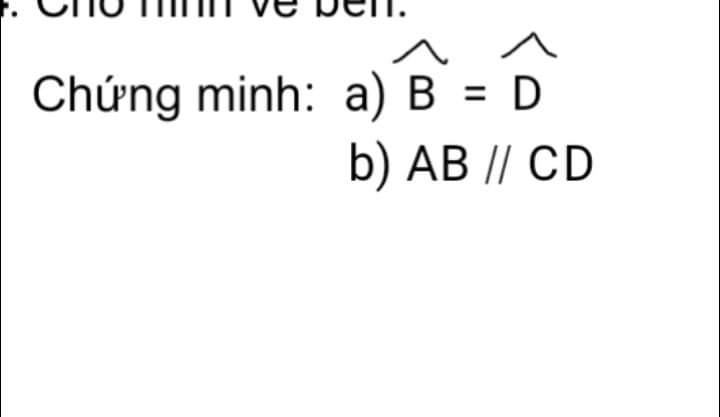
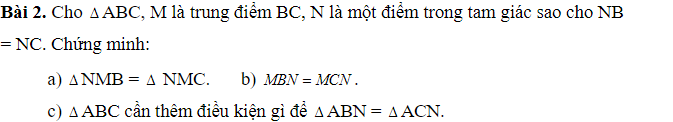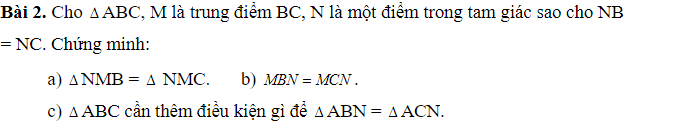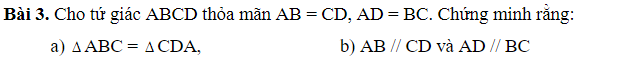a)
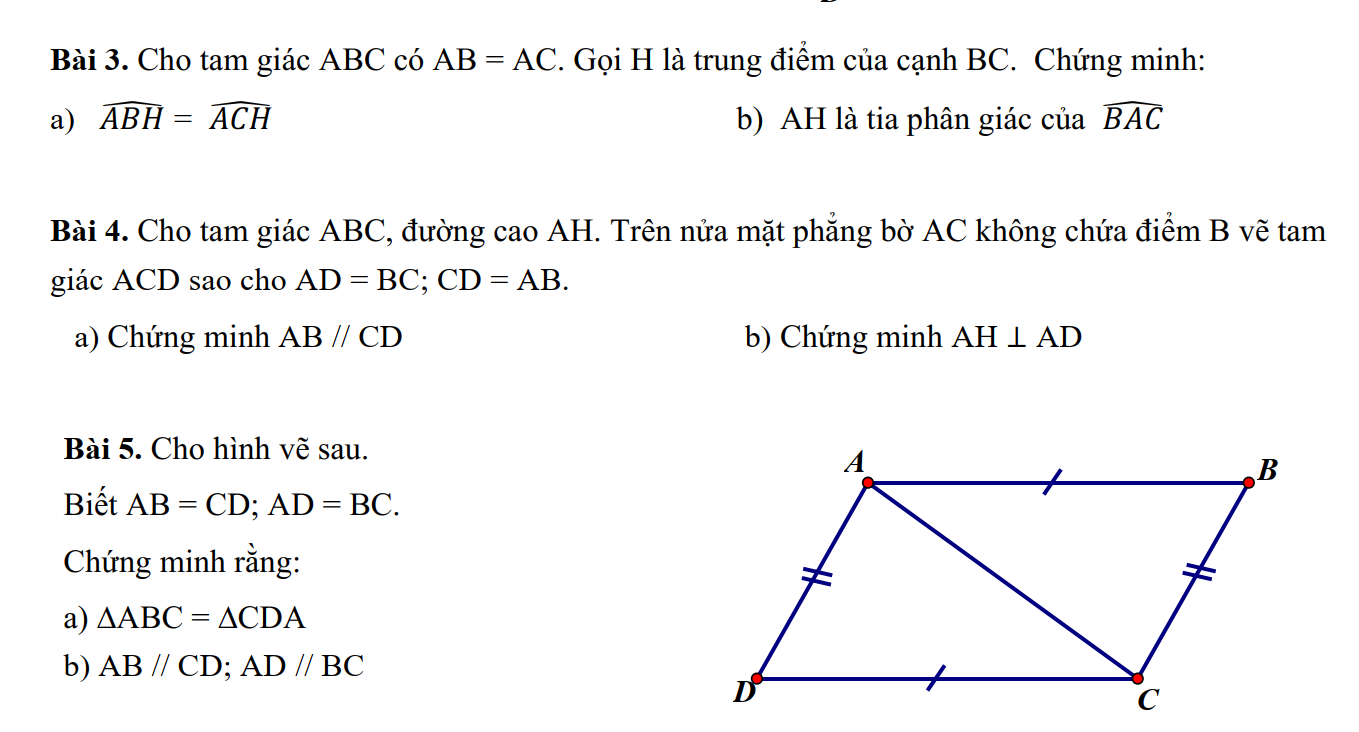
Xét ΔABC và ΔAEF có:
\(AB=AE\left(Gt\right)\)
Chung \(\widehat{A}\)
\(AC=AF\left(Gt\right)\)
⇒ΔABC = ΔAEF (c.g.c)
b) Ta có: \(AF=AC\Rightarrow AB+BF=AE+EC\) mà \(AB=AE\Rightarrow BF=EC\)
ΔABC = ΔAEF (c.g.c)⇒\(\widehat{ACB}=\widehat{AFE}\)( 2 góc tương ứng)
\(AF=AC\Rightarrow\widehat{AFC}=\widehat{ACF}\)
Xét ΔBFC và ΔECF có:
BF=EC (cmt)
\(\widehat{BFC}=\widehat{ECF}\)(cmt)
chung FC
⇒ΔBFC = ΔECF (c.g.c)
⇒\(\widehat{CBF}=\widehat{FEC}\) (2 góc tương ứng)
Xét ΔBDF và ΔCDE có:
\(\widehat{DFB}=\widehat{DCE}\) (cmt)
\(BF=EC\) (cmt)
\(\widehat{FBD}=\widehat{DCE}\) (cmt)
⇒ΔBDF = ΔCDE
c)ΔBDF = ΔEDC (cmb)⇒DF=DC (2 cạnh tương ứng)
Xét ΔADF và ΔADC có:
Chung AD
DF=DC(cmt)
FA=CA (gt)
⇒ΔADF = ΔADC (c.c.c)
⇒ \(\widehat{FAD}=\widehat{CAD}\) (2 góc tương ứng)
d) Xét ΔABD và ΔAEC có:
AB=AE (gt)
\(\widehat{FAD}=\widehat{CAD}\) (cmb)
Chung AD
⇒ΔABD = ΔAEC (c.g.c)