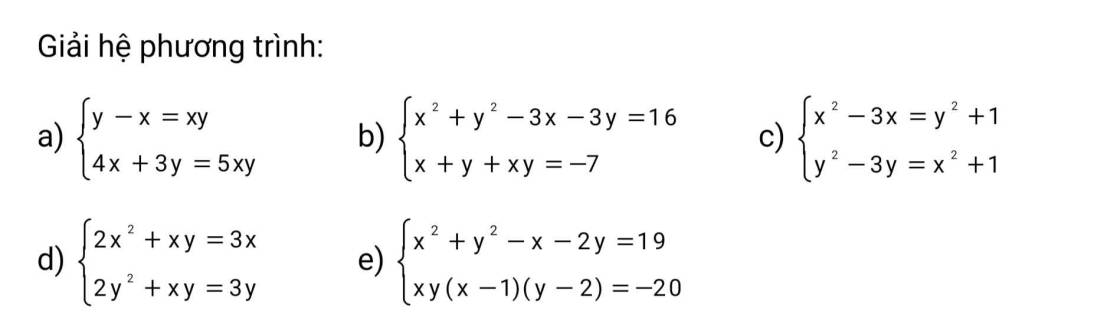ĐKXĐ: \(x^2+4x-1>=0\)
=>\(x^2+4x+4-5>=0\)
=>\(\left(x+2\right)^2>=5\)
=>\(\left[{}\begin{matrix}x>=\sqrt{5}-2\\x< =-\sqrt{5}-2\end{matrix}\right.\)
\(\left(x+2\right)^2-\sqrt{x^2+4x-1}=7\)
=>\(x^2+4x+4-\sqrt{x^2+4x-1}-7=0\)
=>\(x^2+4x-1-\sqrt{x^2+4x-1}-2=0\)
=>\(\left(\sqrt{x^2+4x-1}-2\right)\left(\sqrt{x^2+4x-1}+1\right)=0\)
=>\(\sqrt{x^2+4x-1}-2=0\)
=>\(x^2+4x-1=4\)
=>\(x^2+4x-5=0\)
=>(x+5)(x-1)=0
=>\(\left[{}\begin{matrix}x=-5\left(nhận\right)\\x=1\left(nhận\right)\end{matrix}\right.\)
\(\left(x+2\right)^2-\sqrt{x^2+4x-1}=7\) ( ĐK : \(x\le-2-\sqrt{5}\) hoặc \(x\ge-2+\sqrt{5}\) )
\(pt\Leftrightarrow\left(x+2\right)^2-\sqrt{\left(x+2\right)^2-5}=7\)
Đặt \(\left(x+2\right)^2=a\Rightarrow\sqrt{\left(x+2\right)^2-5}=\sqrt{a-5}\left(a\ge5\right)\)
\(pttt:a-\sqrt{a-5}=7\)
\(\Leftrightarrow\left[{}\begin{matrix}a=11\left(n\right)\\a=4\left(l\right)\end{matrix}\right.\)
+ Với a = 11 :
\(\Rightarrow\left(x+2\right)^2=11\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2+\sqrt{11}\left(n\right)\\x=-2-\sqrt{11}\left(n\right)\end{matrix}\right.\)
Vậy \(S=\left\{-2+\sqrt{11};-2-\sqrt{11}\right\}\)




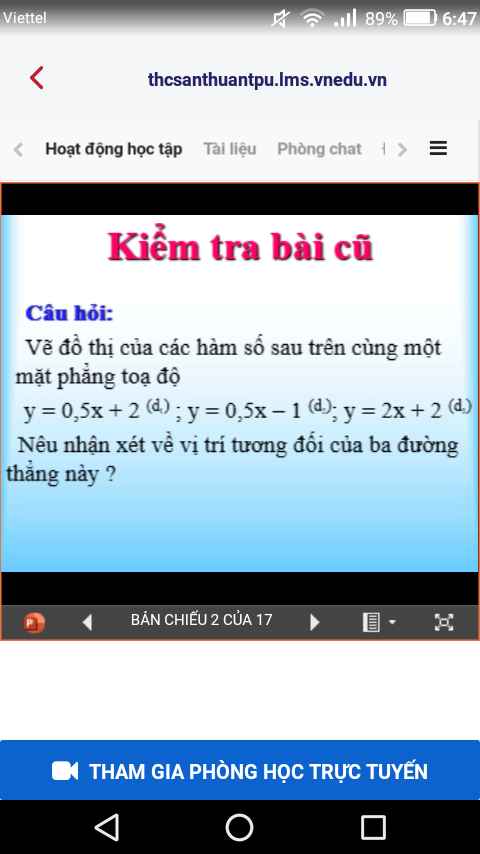

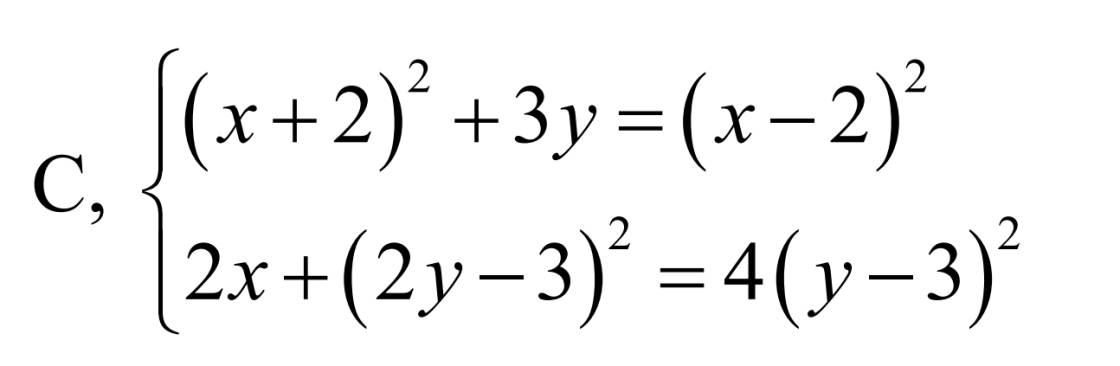


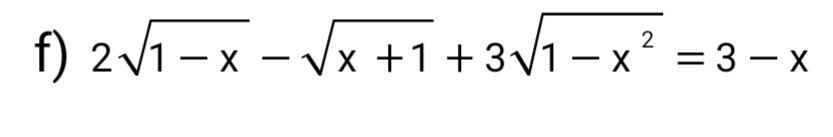 Giải pt . Mn giúp mik vs
Giải pt . Mn giúp mik vs