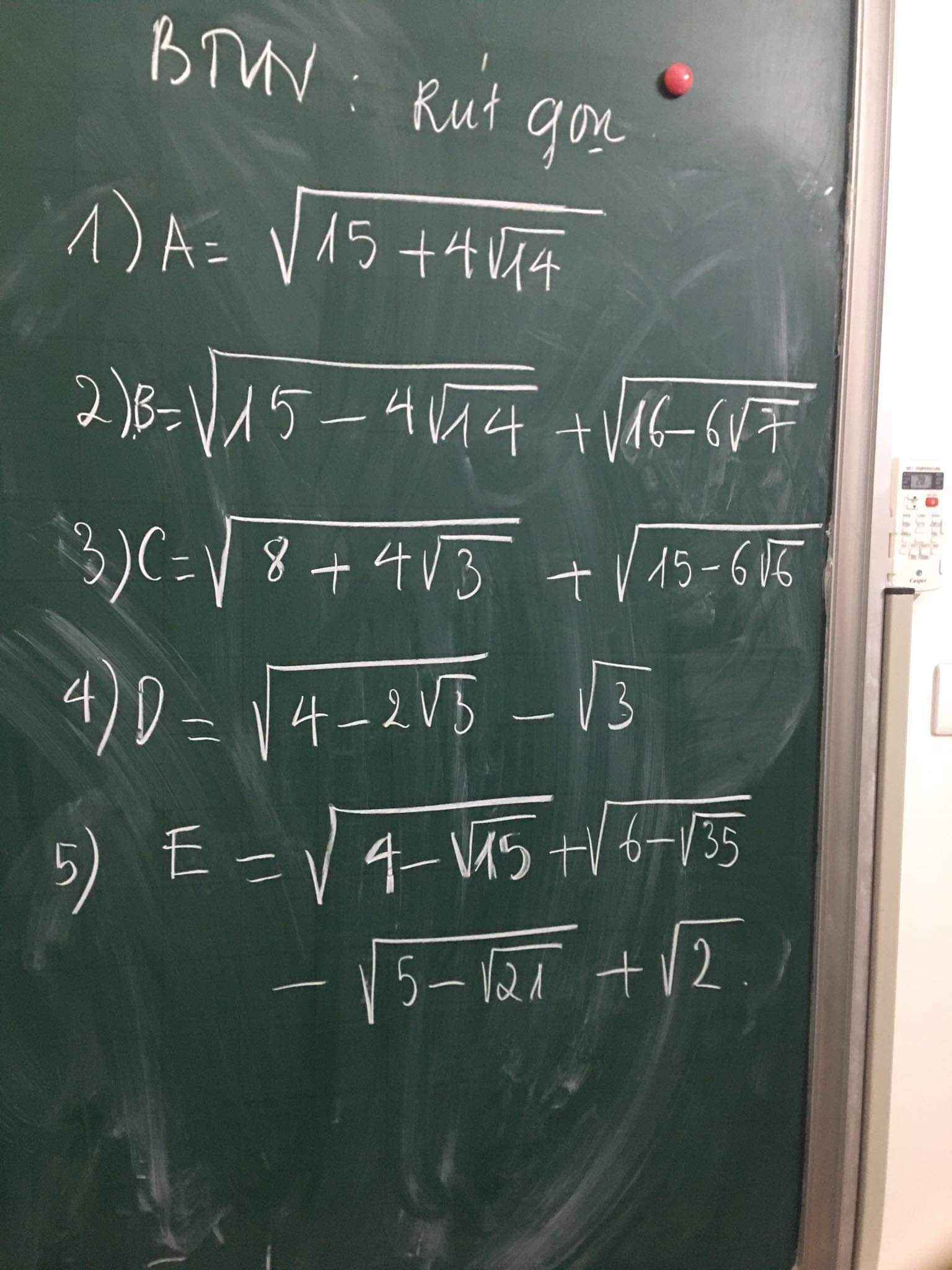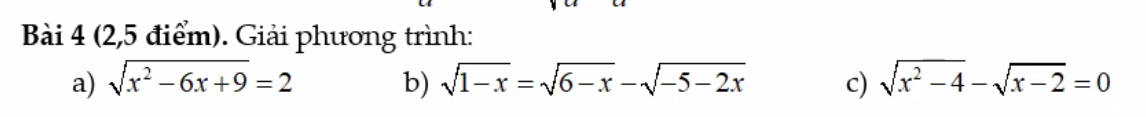câu a, phân tích 4 thành 2.2. căn 14
khi đó 15 sẽ đổi thành 2 bình ( hằng đẳng thức số 2)
tất cả sẽ là: 22 . 2.2.căn 14 . căn 14 bình
các câu sau tương tự nhé có thể làm riêng ra rồi cộng lại nha
e: Ta có: \(E=\sqrt{4-\sqrt{15}}+\sqrt{6-\sqrt{35}}-\sqrt{5-\sqrt{21}}+\sqrt{2}\)
\(=\dfrac{\sqrt{8-2\sqrt{15}}+\sqrt{12-2\sqrt{35}}-\sqrt{10-2\sqrt{21}}+2}{\sqrt{2}}\)
\(=\dfrac{\sqrt{5}-\sqrt{3}+\sqrt{7}-\sqrt{5}-\sqrt{7}+\sqrt{3}+2}{\sqrt{2}}\)
\(=\sqrt{2}\)
1) \(\sqrt{15+4\sqrt{14}}=\sqrt{\left(\sqrt{7}+\sqrt{8}\right)^2}=\sqrt{7}+\sqrt{8}\)
2) \(\sqrt{15-4\sqrt{14}}+\sqrt{16-6\sqrt{7}}=\sqrt{\left(\sqrt{8}-\sqrt{7}\right)^2}+\sqrt{\left(\sqrt{9}-\sqrt{7}\right)^2}=\sqrt{8}-\sqrt{7}+\sqrt{9}-\sqrt{7}=3+2\sqrt{2}-2\sqrt{7}\)3) \(C=\sqrt{8+4\sqrt{3}}+\sqrt{15-6\sqrt{6}}=\sqrt{\left(\sqrt{6}+\sqrt{2}\right)^2}+\sqrt{\left(\sqrt{9}-\sqrt{6}\right)^2}=\sqrt{6}+\sqrt{2}+\sqrt{9}-\sqrt{6}=3+\sqrt{2}\)4) \(D=\sqrt{4-2\sqrt{3}}-\sqrt{3}=\sqrt{\left(\sqrt{3}-1\right)^2}-\sqrt{3}=\sqrt{3}-1-\sqrt{3}=-1\)5) \(E=\sqrt{4-\sqrt{15}}+\sqrt{6-\sqrt{35}}-\sqrt{5-\sqrt{21}}+\sqrt{2}=\sqrt{\left(\sqrt{\dfrac{5}{2}}-\sqrt{\dfrac{3}{2}}\right)^2}+\sqrt{\left(\sqrt{\dfrac{7}{2}}-\sqrt{\dfrac{5}{2}}\right)^2}-\sqrt{\left(\sqrt{\dfrac{7}{2}}-\sqrt{\dfrac{3}{3}}\right)^2}+\sqrt{2}=\sqrt{\dfrac{5}{2}}-\sqrt{\dfrac{3}{2}}+\sqrt{\dfrac{7}{2}}-\sqrt{\dfrac{5}{2}}-\sqrt{\dfrac{7}{2}}+\sqrt{\dfrac{3}{2}}+\sqrt{2}=\sqrt{2}\)
3: Ta có: \(\sqrt{8+4\sqrt{3}}+\sqrt{15-6\sqrt{6}}\)
\(=\sqrt{6}+\sqrt{2}+3-\sqrt{6}\)
\(=3+\sqrt{2}\)
4: Ta có: \(D=\sqrt{4-2\sqrt{3}}-\sqrt{3}\)
\(=\sqrt{3}-1-\sqrt{3}\)
=-1